Mein Leben / Leo Koenigsberger

Berlin 1857 - 64

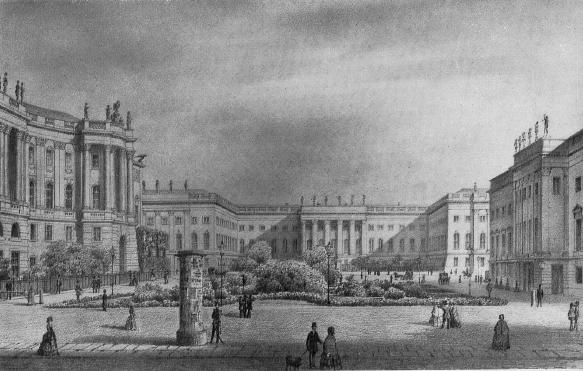
Opernplatz mit Universität / F. A. Borchel, um 1860
Quelle: Vom Prinzenpalais zur Humboldt-Universität / Klaus-Dietrich Gandert. - 1985, S. 74
UB Heidelberg: 85 A 18244

(Seite 21) Nachdem ich das Maturitätsexamen bestanden, durch eine Prämie (Müllers Kosmische Physik) ausgezeichnet worden, und von Marquardt ein recht gutes Abiturientenzeugnis erhalten hatte, das mit den Worten schließt:

„Die Prüfungskommission entläßt ihn mit dem Wunsche, daß er, auf dem betretenen Wege rüstig fortschreitend, den erregten Erwartungen zu entsprechen bemüht sein werde,“

Dirichlet war bereits in Göttingen, Kummer sein Nachfolger in Berlin, und Weierstraß, der erst kurz vorher von Braunsberg an das Berliner Gewerbe-Institut berufen war, hatte als außerordentlicher Professor an der Universität erst im Winter 56/57 eine kleinere Vorlesung über die Gaußsche Theorie der Dispersion gehalten, die Fuchs mit (Seite 22) sehr wenigen anderen Zuhörern auch gehört hat. Als ich Ostern 57 nach Berlin kam, war ich so weit vorbereitet, daß ich Weierstraß' erste Vorlesung über die Theorie der elliptischen Funktionen hören konnte, von deren Inhalt ich als einziger noch lebender Zuhörer erst vor zwei Jahren eine kurze Skizze^(2.2) veröffentlicht habe. Die geringe Zahl der Zuhörer in dieser Vorlesung hatte sich allmählich auf 4 bis 5 Hörer reduziert, zu denen auch Fuchs und bisweilen Bolzani gehörten, der Professor der Physik an der russischen Universität Kasan, den mehrere Jahre vorher Lobatschefskij hinter dem Ladentisch einer Konditorei damit beschäftigt fand, ein mathematisches Buch zu lesen, und dem er den Eintritt in das Gymnasium und dann den Besuch der Universität ermöglichte. Weierstraß machte gleich in der ersten Vorlesung auf mich einen mächtigen, unvergeßlichen Eindruck; in dem rauhen Aprilwetter trat der schon durch seine äußere Erscheinung uns imponierende verehrte Meister jedesmal in schweren Galoschen, den Hals mit einem dicken Tuche umhüllt, fast immer befangen und verlegen auf das Katheder, auf dem er zunächst ein ganzes Paket von beschriebenen Quartblättern ausbreitete, die in kürzester Zeit in solche Unordnung gerieten, daß öfter ein Teil der Stunde durch das fortwährende Zusammensuchen derselben für den Vortrag verloren ging. Die Vorlesung begann mit dem Additionstheorem der ϑ-Funktionen, behandelte die Eigenschaften dieser Funktionen für die einfachsten Beziehungen der ϑ-Moduln und führte weiter zu den Beziehungen, welche zwischen dem zweiten (Seite 23) logarithmischen Differentialquotienten einer ϑ-Funktion und dem Quotienten zweier solcher Funktionen selbst bestehen. Um den Übergang zur Umkehrung des elliptischen Integrals erster Gattung zu machen, wurde der Modul des Integrals in der Legendreschen Normalform als reell vorausgesetzt, und erst fast am Ende der Vorlesung die Ausdehnung auf beliebig komplexe Werte desselben in einer für uns — wenigstens für mich, den einsemestrigen Studenten — nicht ganz verständlichen Weise durchgeführt, da Weierstraß, wie früher auch Jacobi in seinen Vorlesungen in Königsberg, die komplexe Integration zu vermeiden suchte, ihrer aber doch nicht ganz entraten konnte. Nach der Diskussion der Nullen und Unendlichkeitswerte der drei elliptischen Funktionen schloß die Vorlesung, welche durch die nicht seltene Ankündigung von Weierstraß „morgen ist katholischer Feiertag“ häufige Unterbrechungen erfuhr, mit der Behandlung des Abelschen Theorems für elliptische Integrale, das er in analoger Weise in einer Fortsetzung im Wintersemester, auf hyperelliptische Integrale ausdehnte, zugleich behandelte er noch in einer kleineren Vorlesung einige Anwendungen der elliptischen Funktionen auf das Pendelproblem und die geodätische Linie auf dem elliptischen Erdsphäroid in überaus eleganter Weise, welche später durch den Gedanken, x+yi und z als elliptische Integrale der Zeit auszudrücken und das Problem durch Zerlegung einer ϑ-Funktion eines komplexen Arguments in den reellen und imaginären Teil zu lösen, für die Behandlung ähnlicher geometrischer und mechanischer Probleme vorbildlich (Seite 24) wurde. Seine Vorlesungen über elliptische Funktionen leiteten eine völlig neue Ära für die mathematischen Studien an der Berliner Universität ein und reihten sich an die Glanzzeit von Jacobi und Dirichlet, deren Vorlesungen über elliptische Funktionen, Zahlentheorie und bestimmte Integrale von den mathematischen Hörern bisher schmerzlich vermißt wurden; Kummer legte, von seinen kleineren ausgezeichneten Vorlesungen über spezielle Teile der höheren Zahlentheorie und der Flächenlehre abgesehen, in seinen größeren Vorlesungen über Mechanik, analytische Geometrie u. a. mehr Wert darauf, die elementaren Teile dieser Disziplinen, freilich mit unvergleichlicher Klarheit, seinen Zuhörern zu übermitteln, und Arndt sowie Hoppe hielten nur kleine und wenig besuchte Vorlesungen.

Fuchs war während seiner Studienzeit Kummer auch persönlich näher getreten, und dessen Vorlesung über die Theorie der krummen Linien und Flächen veranlaßten ihn, sich auf seinen Rat als Thema der Dissertation die Aufsuchung der Krümmungslinien für verschiedene Flächengattungen zu wählen. Kummer hatte ihn zunächst auf das Studium von Monge's applications de l'analyse à la géométrie hingewiesen, aber die Anschaffung dieses Werkes erforderte eine für seine Verhältnisse damals unerschwingliche Ausgabe; auf den Leihzetteln der königlichen und Universitäts-Bibliothek fand sich stets der Vermerk „verliehen“, und auch ich war erst, nachdem ein Teil seiner Dissertation bereits fertig gestellt war, in der Lage, mir dieses Werk antiquarisch zu erwerben. So trat Fuchs, meist nur (Seite 25) mit den aus Cournot gewonnenen Kenntnissen ausgerüstet, an die Behandlung der Aufgabe heran, und es gelang ihm, nachdem er manches, was bereits bekannt war, wiedergefunden, durch selbständige und geistvolle Überlegungen die Krümmungslinien neuer Flächengattungen zu ermitteln. Weingarten, damals noch Lehrer an der Gewerbeschule, später eine der Zierden der Berliner technischen Hochschule, ein stud. Fischer und ich, der dreisemestrige Student, waren Opponenten in den damals noch üblichen Kontroversen der öffentlichen Disputation bei der am 2. August 58 mit der Dissertation:  „De superficierum lineis curvaturae“  erfolgten Promotion. Während nun Fuchs, nachdem er unmittelbar darauf sein Oberlehrerexamen gemacht, Hilfslehrerstellen an der Gewerbeschule und der Luisenstädtischen Realschule bekleidete, hörte ich in den folgenden Semestern außer einer physikalischen und philosophischen Vorlesung bei Dove und Trendelenburg noch die wenigen übrigen mathematischen Vorlesungen, welche die Berliner Universität damals bot, studierte aber um so eifriger die Werke von Gauß, Lagrange u. a., welche allmählich durch Geschenke in meinen Besitz gekommen waren, und indem ich noch Kenntnisse sammelte, beschäftigte sich Fuchs bereits mit seinen ersten zahlentheoretischen Untersuchungen im Anschluß an die berühmten Kummerschen Arbeiten über ideale Zahlen.

Die Zahl unserer Bekannten war gering; wiewohl noch Student wurde ich von Fuchs in ein kleines mathematisches Kränzchen eingeführt, dem früher auch Riemann angehörte, und in dem sich (Seite 26) jetzt regelmäßig die Mitglieder versammelten: Bertram, der sich duch eine Arbeit über die geometrische Darstellung des reellen und imaginären Teiles der elliptischen Funktion eines komplexen Argumentes bekannt gemacht, Fuchs, ferner der ausgezeichnete theoretische Physiker an der Universität Jochmann, der Professor am Kölnischen Gymnasium, Hermes, Verfasser einer größeren Zahl geometrischer Arbeiten und später der verdienstvolle Herausgeber des geometrischen Nachlasses von Jacobi, und endlich Natani, der scharfsinnige Verfasser einer Reihe von Arbeiten über partielle Differentialgleichungen und von einzelnen Artikeln in einem mathematischen Lexikon, welche, auch selbständig erschienen, zu unsern besten Lehrbüchern gehören. Wir fanden uns wöchentlich zu einem kürzeren Vortrage im Hause von Bertram ein, um dann bei einem Glase Bier, meist in Gesellschaft von Weingarten, einige Stunden in wissenschaftlicher Unterhaltung zu verplaudern, die sich bisweilen zu einer recht scharfen Kritik der neu auftauchenden mathematischen Talente der Göttinger und Berliner Schule zuspitzte.

Inzwischen hatte ich schon in meinem 4. Semester das Glück gehabt, Weierstraß näher treten zu dürfen; als er sich damals bereits mit der Einführung seiner σ-Funktion beschäftigte, ließ er mich für die Transformation 3. und 5. Grades die Berechnung der Modulargleichungen in den Invarianten ausführen, umd am Anfange meines 5. Semesters schlug er mir als Thema für eine Dissertation die Zurückführung der Langrangeschen Bewegungsausdrücke (Seite 27) eines von zwei festen Zentren nach dem Newtonschen Gesetze angezogenen Punktes auf ϑ-Funktionen vor; am 22. Mai 1860 wurde ich unter Assistierung der Opponenten Fuchs und zweier Zuhörer von Weierstraß, Herzberg und Lieber, mit der Dissertation:  „De motu puncti versus duo fixa centra attracti“^(2.3) promoviert. Es war ein sonderbares mündliches Doktorexamen gewesen, welches in der Mathematik von zwei Examinatoren, Martin Ohm und Kummer, in der Physik von Magnus, in der Philosophie von Trendelenburg abgenommen wurde, und der Komik nicht ganz entbehrte. Bei dem Besuche, den ich Ohm vor der Prüfung machte, hatte er mich gefragt, womit ich mich in meiner Studienzeit besonders beschäftigt habe, und als ich ihm die Theorie der elliptischen Funktionen bezeichnete, erklärte er sich bereit, mich in diesem Zweige der Analysis zu examinieren. Vor Beginn der Prüfung jedoch teilte er mir im Vorzimmer des Prüfungssaales mit, daß er mich in andern Teilen der Mathematik examinieren und es Kummer überlassen werde, mich aus der Theorie der elliptischen Funktinen zu prüfen. So glaubte ich nun nach seiner Prüfung in der Mechanik, die sich lediglich um die Gleichgewichtsbedinungen eines festen Systems drehte und durch die Pedanterie in der Aufzählung aller denkbar möglichen Fälle auf den ein wenig zaghaften Examinanden einen erheiternden Eindruck machte, allen seinen Quälereien entgangen zu sein, als er plötzlich ganz unvermittelt zu den Prinzipien der Differentialrechnung überging, einem gefürchteten Ohmschen Prüfungsgegenstand. Nun gab es (Seite 28) ein Hin- und Herreden über Konvergenz und Divergenz der Reihen zwischen dem Examinator und mir, der ich zuerst Ohm zu widersprechen wagte, bis dieser mit den Worten schloß: „Nun werden Sie wohl auch von der Richtigkeit meiner Behauptung überzeugt sein.“ „Sie werden es besser wissen, als ich, Herr Professor“ war die Antwort des eingeschüchterten Examinanden. Mit ironischem Lächeln, dessen Deutung leicht ersichtlich war, begann der seinen Kollegen so unendlich überragende Kummer sein Examen, in dem ich eine längere Reihe von Fragen aus der Theorie der komplexen Multiplikation der elliptischen Transzendenten zu beantworten hatte, was mir zu dessen Zufriedenheit gelang. Da auch Magnus und Trendelenburg mit mir recht zufrieden waren, glückte es mir ein  „magna cum laude“  zu erringen.

Nach Absolvierung des Doktorexamens meldete ich mich sogleich zur Oberlehrerprüfung, die ich in der Mathematik und Physik bei dem ausgezeichneten Pädagogen und sehr kenntnisreichen Mathematiker Schellbach ablegte; ich erhielt von ihm die facultas in Mathematik und Physik für die oberen Klassen mit dem Zeugnis:

„der Candidat hielt in der Prima eines Gymnasiums eine mathematische Probelection über die Convergenz der Reihen ab, bewies entschiedenes Geschick in der Behandlung des Lehrstoffs und zeigte zugleich ein so lebhaftes Interesse für die Lösung seiner Aufgabe, daß seine Einwirkung auf die Schüler eine entschieden günstige zu nennen war. In der mündlichen Prüfung zeigte sich der Candidat sehr (Seite 29) bald als ein Mathematiker, dessen Kenntnisse namentlich in den schwierigeren Theilen der Integralrechnung einen ungewöhnlich hohen Grad von Klarheit und Sicherheit besitzen. Auch die verschiedenen Theile der höheren Geometrie sind ihm größten Theiles sehr vollständig bekannt, und ebenso vertraut ist er auch mit der Theorie der Integrale der Differentialgleichungen. Ebenso gründlich hat er die theoretische Mechanik studiert, und in all den genannten Disziplinen waren nur selten Lücken in seinem Wissen zu bemerken.“

Meinecke fand meine „Reminiscenzen im Lateinischen und Griechischen völlig genügend, um mir die facultas bis zur Untersekunda zu ertheilen,“ nur Trendelenburg wünschte, daß ich „für die Fragen der wissenschaftlichen Pädagogik und Didaktik noch mehr in die Psychologie eingehe.“

Schellbach nahm mich nun auf Grund meines Examens nach einer Probelektion, die ich in der Prima des Gymnasiums zu seiner Zufriedenheit abgehalten, in sein mathematisch-pädagogisches Seminar am Friedrich-Wilhelms-Gymnasium auf, an dem man zur Ableistung des Probejahrs nur ein halbes Jahr tätig zu sein brauchte, und gab mir nach Absolvierung desselben das nachfolgende Zeugnis:

„Herr Dr. K. hat in den drei oberen Klassen des Gymnasiums unter meiner Leitung in den verschiedensten Disciplinen Unterricht ertheilt. Der Umfang seiner Kenntnisse und die Sicherheit, mit der er sie zur Anwendung bringt, verschaffen seinen Lehrstunden einen ungewöhnlich günstigen Erfolg, den man auch der Lebendigkeit seines Vortrages^(2.4) zuschreiben (Seite 30) muß, die aus einem entschiedenen Interesse an pädagogischer Thätigkeit entspringt. Nach meiner Überzeugung wird sich Herr Dr. K. in kurzer Zeit zu einem unserer tüchtigsten Gymnasiallehrer ausbilden, wenn ihm Gelegenheit gegeben wird, noch weitere pädagogische Erfahrungen zu sammeln.“

Aber ich muß hierbei hervorheben, daß der mathematische Unterricht von Schellbach stets einen ungewöhnlichen Erfolg hatte und daher das Interesse der Schüler auch einem anderen Lehrer von selbst entgegenkam. Von den vielen dortigen vortrefflichen Schülern, denen ich noch später begegnete, nenne ich nur Felix Müller, von dem ich 10 Jahre später bei Gelegenheit seiner Gründung der „Fortschritte der Mathematik“^(2.5) die folgenden Zeilen erhielt:

„Als ich noch auf den Bänken des hiesigen Friedrich-Wilhelms-Gymnasiums saß, hatte ich die Ehre, auch Ihren Unterricht zu genießen. Doch ist seit jener Zeit fast ein ganzen Decennium vergangen, so daß ich nicht erwarten darf, mich Ihrer Erinnerung erfreuen zu dürfen; inzwischen war ich auch Mitglied des Schellbachschen Seminars......“.

Diesem Umstande habe ich wohl auch zum Teil die nachsichtige Besprechung meiner Arbeiten über elliptische Funktionen in seiner verdienstvollen Neubearbeitung der Geschichte dieser Transzendenten von Enneper zu verdanken.

Aber meine glückliche und rasche Überwindung der verschiedenen Stadien aller dieser Prüfungen konnte die Hindernisse nicht aus dem Weg räumen, welche in der politischen und kirchlichen Anschauungen (Seite 31) der damaligen Blütezeit der Reaktion tief begründet waren, und welche auch Fuchs noch immer in seiner schweren und dürftigen Stellung als nicht etatmäßigen Hilfslehrer festbannten. So mußten Fuchs und ich sich die Frage vorlegen, ob wir den herrschenden, engherzigen Anschauungen der Regierung unser ganzes wissenschaftliches Leben und unsere Existenz überhaupt zum Opfer bringen oder, nachdem wir längst alle religiösen Vorurteile abgestreift, zum Christentum übertreten sollten. Fuchs hatte bereits drei Jahre in ewigem Zaudern und Schwanken verstreichen lassen, da er Rücksichten der verschiedensten Art auf seine Familie nehmen mußte, während ich, da mein elterliches Haus jeder streng religiösen Richtung fern stand, von derartigen Fesseln frei war; und so hatte mein fester Vorsatz auch für Fuchs, der sein ganzen Leben hindurch bei jedem entscheidenden Entschlusse ängstlich und zaghaft gewesen, die Folge, daß auch seine Zukunft gerettet wurde. Durch unsere verehrten Lehrer Kummer und Weierstraß in unserer Absicht bestärkt, traten wir beide, dank dem von wahrhaft religiöser und im edelsten Sinne freiheitlicher Gesinnung getragenen Entgegenkommen des Predigers Müllensiefen in unserm Gewissen nicht beschwert, zum Christentum über. Von uns jüngeren Mathematikern, die sich in ähnlicher Lage befanden, war es nur Hamburger, dem mancherlei Rücksichten diesen Schritt erschwerten, und der infolge davon fast sein ganzes Leben hindurch in einer seiner Bedeutung wenig würdigen Stellung für seine und seiner Familie Existenz kämpfen mußte. Aber auch (Seite 32) jetzt waren noch nicht alle Hindernisse für uns überwanden: stand auch an der Spitze des preußischen Schulwesens der, wenn auch streng kirchliche und reaktionäre, so doch durchaus gewissenhafte und hochverdiente Schulmann Wiese, so waren doch viele der ihm untergeordneten Schulräte und Direktoren bestrebt, die vornehme Gesinnung Wieses in orthodoxem Sinne auszubeuten und bis in die intimsten Familienverhältnisse der ihnen ausgelieferten Schulamtskandidaten sich einzumischen, wenn diese sich nicht energisch dagegen wehrten. Noch längere Zeit mußte Fuchs in seiner prekären Stellung ausharren, während mir, der ich mich nicht auf unabsehbare Zeit als Hilfslehrer in eine kleine Provinzialstadt schicken lassen wollte, um mit Weierstraß noch länger in Verbindung bleiben zu können, durch die Fürsprache von Schellbach eine, wenn auch nicht etatmäßige, Stellung als Lehrer der Mathematik und Physik am Berliner Kadettenkorps^(2.6) angeboten wurde, die ich dann von Ostern 61 bis Ostern 64 bekleidete.

Freilich fiel mir der Unterricht in der Physik zuerst nicht leicht. Ich hatte, wie es damals bei Studierenden der Mathematik fast ausnahmslos der Fall war, auf der Universität nie einen Apparat in Händen gehabt und sollte nunmehr in vier Parallelklassen der Sekunda und Prima des Korps Experimentalphysik vortragen; die gern gewährte und tatkräftige Unterstützung von seiten meiner Kollegen Paalzov und Erdmann sowie andauernder Fleiß und stundenlange tägliche Übung ließen mich jedoch die Schwierigkeiten für den immerhin elementaren (Seite 33) Unterricht leicht überwinden, so daß mir meine pädagogische Tätigkeit an dem militärischen Institute recht viel Freude bereitete. Der Chef des Korps, General v. Ollech, war eine in äußeren Formen zwar strenge, im Grunde jedoch vornehme, durch und durch humane und, wie seine geschichtlichen Studien zeigten, auch wissenschaftlich veranlagte Natur, der Studiendirektor v. Wartenberg ein Mann von feinem Takt und gewinnenden Manieren, die Abteilungsvorstände durchweg tüchtige, im besten Sinne preußische Militärs, und die Kadetten im Durchschnitt bescheiden und nicht weniger beanlagt und lernbegierig als die Schüler anderer Mittelschulen, wenn man die mir Recht völlig verschiedenen Anforderungen berücksichtigt — damals ahnte ich nicht, daß ich zehn Jahre später die Namen so vieler von diesen, in den Annalen der Geschichte Deutschlands ruhmbedeckt, wiederfinden würde, und noch in den letzten Jahren brachte dem nunmehr gebrechlichen Greise aus den Kämpfen des unseligen Krieges der Jubel des Volkes so manchen Namen aus damaliger Zeit wieder in lebhafte Erinnerung! Aber ich mußte mich freilich zunächst an die strenge militärische Ordnung gewöhnen; „lieber Herr Doktor — sagte Ollech, nachdem er einer meiner ersten physikalischen Unterrichtsstunden beigewohnt, in der ich bei einer theoretischen Auseinandersetzung am Katheder stehend meinen Kopf einige Zeit auf den Arm gestützt hielt — Sie dürfen es mir nicht übel nehmen, wenn ich Ihnen, dem jungen Manne gegenüber die Bitte auszusprechen wage, sich beim Unterricht ein wenig strammer zu halten, da unsere Kadetten (Seite 34) es bei ihren militärischen Lehrern und Erziehern so gewöhnt sind“ — und ich nahm die Ermahnung nicht übel auf; dafür wies er aber auch die Denunziation eines später jammervoll verkommenen Kadettenhauspredigers barsch ab, als dieser ihm eine freisinnige politische Äußerung, die ich in Gegenwart befreundeter Offiziere im Lehrerzimmer getan, in gehässiger Weise hinterbrachte. Es ist mir heute noch und vielleicht heute erst recht nach all' den großen Ereignisses der Jahre 70/71 und den für die Geschichte Preußens und Deutschlands so traurigen Geschicken unserer heutigen Zeit eine freudige Erinnerung, wenn ich all die Männer wie den Prinzregenten Wilhelm, den Studiendirektor des preußischen Militärwesens v. Peucker, den General v. Manteuffel u. a. an meiner Seele vorüberziehen lasse, wie sie alljährlich zu den Prüfungen erschienen, um in liebenswürdiger Weise von den Erfolgen unseres Unterrichts Kenntnis zu nehmen, und in längerer oder kürzerer Rede die Kadetten auf die Bedeutung der militärischen Bildungsanstalten für die Zukunft des preußischen Staates hinzuweisen — das Schicksal hat es anders gewollt, und mit so vielem Schlechten und Verdammenswerten auch manches Schöne und Erfolgverheißende dem Untergange geweiht.

Ich will aber auch nicht leugnen, daß wir Zivillehrer in der damals so aufgeregten Konfliktzeit hin und wieder ein gewisses Unbehagen in unserer Stellung empfanden, denn wir gehörten sämtlich der grollenden Fortschrittspartei^(2.7) an, teilten die Ansichten der damaligen Volkszeitung und hörten häufig im (Seite 35) Handwerkerverein die aufregenden Reden von Johann Jacobi, Virchow, Twesten u. a., welche die entschiedensten Gegner aller militärischen Erziehungsinstitute waren.

Da ich täglich 4 bis 5 Unterrichtsstunden im Kadettenkorps zu geben hatte, außerdem täglich die physikalischen Experimente sorgfältig vorbereiten mußte, endlich noch Privatstunden zu erteilen genötigt war, so waren es hauptsächlich die Abend- und Nachtstunden, die mir in den nächsten vier Jahren für mathematische Studien übrig blieben.

Häufig kamen in dieser Zeit Fuchs und ich mit Roethig, dem Verfasser einiger schönen Potentialarbeiten, sonders aber mit Natani, Weingarten, Paul du Bois-Reymond und Hamburger, die nicht Mitglieder unseres Kränzchens waren, meist in dem Bierlokal von Donny am Dönhofsplatz — der Arbeitsstätte von Natani, Weingarten und du Bois — zusammen, um einige Stunden in anregender und fruchtbringender, wissenschaftlicher Unterhaltung zu verplaudern.

Sie waren sämtlich Originale in ihrer Art. Den bedeutendsten Eindruck machte auf uns alle Natani, der bei weitem älteste von uns; noch ein Schüler Eisensteins aus der Zeit, in der dieser geniale Mathematiker bei seiner ungeordneten Lebensführung noch seine Vorlesungen vor 3 bis 4 Zuhörern in seiner Wohnung im Bette liegend hielt, zugleich ein treuer Zuhörer Dirichlets, besaß er umfangreiche Kenntnisse in der Mathematik und mathematischen Physik, eine überraschend schnelle Auffassungsgabe für die schwierigsten Fragen und (Seite 36) einen ungewöhnlichen Scharfsinn in der Behandlung derselben — eine einfache, durch und durch wahre Natur, bescheiden, aber häufig auch sarkastisch, fast ganz auf den Verkehr mit uns beschränkt. Im April 1889 schrieb er mir:

„Lieber Professor und Freund! Meinen besten Dank für die gütige Erinnerung an mein zurückgelegtes 14. Lustrum oder 140. Semester. Zu versichern brauche ich Ihnen nicht, daß unser Zusammenleben eine der angenehmsten Erinnerungen für mich ist und während meiner noch übrigen Lebenszeit, die freililch nach einer mittels der Methode der kleinsten Quadrate angestellten Wahrscheinlichkeitsrechnung sich als sehr klein ergibt, bleiben wird. Für diese Erinnerung wird mir das gütigst übersandte Bild ein liebes Denkmal sein. ....“.

Ich sah ihn nur noch einmal in Wien wieder, nachdem es ihm nach vielen vergeblichen Versuchen, sich eine feste Lebensstellung zu verschaffen, gelungen war, ein sehr geschätzter Lehrer an der vereinigten Artillerie- und Ingenieurschule in Berlin zu werden; wann er seine Stellung aufgegeben, darüber bin ich ohne Kenntnis geblieben; er starb 1905 im Alter von 86 Jahren.

Von diesem in seinen Formen nicht immer korrekten Freunde unseres Kreises unterschied sich wesentlich der weit geschmeidigere, in seiner Beurteilung von Personen und Dingen viel schärfere geniale Mathematiker Weingarten. Ein wenig verbittert dadurch, daß er nach den Anschauungen der damaligen Zeit, da er ein Maturitätsexamen am Gymnasium nicht abgelegt, als Privatdozent zur (Seite 37) Universität nicht zugelassen werden konnte, und daher, wenn auch wenig zum Mittelschullehrer geeignet, viele Jahre in einer ihm durchaus nicht zusagenden Beschäftigung festgehalten wurde, hatte er schon als junger Mann, von Dirichlet angeregt, seine glänzenden Anlagen in scharfsinnigen Untersuchungen über Fragen der Potentialtheorie betätigt; erst spät war es ihm gelungen, eine Professur an der technischen Hochschule in Berlin zu erlangen, und sich mit Ruhe wissenschaftlicher Arbeit zu widmen, die auf dem von Gauß fundamentierten Gebiete der krummen Flächen die glänzendsten Resultate zeitigte. Ich habe ihn im Laufe der Jahre öfter in der Schweiz im Kreise seiner Frau und Kinder gesehen und war später durch das tragische Ende seines Familienglücks überaus traurig berührt worden, wenn ich auch bei dem unsteten Charakter dieses ausgezeichneten Mannes einen solchen Lebensabschluß nicht überraschend fand. Kurz vor seinem Tode schrieb er mir im Januar 1908 aus Freiburg, wohin er sich zurückgezogen hatte:

„Mit Ihrer freundlichen Neujahrskarte haben Sie mir eine große Freunde gemacht, für die ich Ihnen aufrichtig danke. Bilder aus alter Vergangenheit sind in meinem Gedächtnis aufgetaucht. Aber auch wieder das leidige Gefühl, alt geworden zu sein. Was konnte man damals alles in sich aufnehmen! Wenn ich heute Neues lese, so habe ich das Gefühl, daß mir die Fingerfertigkeit abgeht, das Neue zu verwerten, daß ich es nicht werde gebrauchen können für einen eignen Gedankengang, und daß ich zu alt bin, um zu lernen, wie schön auch immer (Seite 38) das Gelesene sein mag. Das ist ein peinliches Gefühl. Ehemals hielt ich Jemanden von diesem Geisteszustand für ein Rindvieh, heute muß ich zufrieden sein, daß ich noch als ein solches Rindvieh existiere. So ändern sich die Zeiten ! ..... Als ich duch das liebenswürdige Interesse, das Lüroth an mir nahm professor honorarius in Freiburg wurde, erinnerte ich mich des guten alten Fuchs; er sagte einmal (vor 40 Jahren, als er noch Lehrer bei Gallenkamp war): „Ja Weingarten, aus uns wird nichts; ich werde einmal noch Professor werden, aber mit 70 Jahren außerordentlicher Professor in Tübingen“; Tübingen nahm damals für ihn die letzte Stelle unter den Universitäten ein. Nun bin ich mit 70 Jahren doch Universitätsprofessor geworden; er hat es nicht mehr erlebt, er hätte sich darüber amüsiert. Wie viele aus unserer alten Zeit sind schon in das Jenseits hinübergegangen, wie wenige Mathematiker aus dieser Zeit leben noch, an denen man auch persönliches Interesse hat!“

Er starb mit sich und seinem Schicksal zerfallen in seinem 74. Lebensjahr.

Ganz anders der in seiner äußern Erscheinung ein wenig schwerfällige, jeglicher Art geistigen und materiellen Genusses zugängliche Paul du-Bois-Reymond, der Bruder des berühmten Berliner Physiologen Emil du-Bois-Reymond, welcher die geistige Superiorität seines Bruders auf dem Gebiete der Mathematik nicht nur sondern auch auf dem der Philosophie stets und gern anerkannte. Ein feinsinniger Kenner der Kunst, eine durch und durch philosophisch angelegte Natur machte er sogleich die (Seite 39) Grundprinzipien der Integralrechnung zum Gegenstand seiner Forschungen, und war später, nachdem er sich bisweilen zu einem Mystizismus in der Betrachtung rein mathematischer Materien hatte hinreißen lassen, einer der ersten Anhänger und Fürsprecher der die neue Mathematik beherschenden philosophischen Anschauungen von Georg Cantor. Auch er war seiner ganzen Natur nach, ebenso wie Natani und Weingarten, zum Erzieher der Schuljugend nicht geschaffen, gelangte aber erst spät zu einer ihn befriedigenden akademischen Stellung; ich fand ihn im Jahre 69 in der Stellung eines außerordentlichen Professors in Heidelberg wieder. Ernst und Humor vereinigten sich von Jugend auf in dieser reich beanlagten Natur; so schrieb er mir auf meine mündliche Anfrage in unserm Kränzchen im Jahre 62:

„Geehrter Herr Dr.! ...... es erhält überhaupt das Integral einer Differentialgleichung (von der Sorte, die wir meinen), sucht man es mit der allgemeinen Substitution y-y₀ = a(x-x₀) auf, stets die elegante Form f(x,y,z) = f(x₀,y₀,z₀). Entschuldigen Sie diesen Wisch, aber ich durfte Ihnen diese Rechtfertigung nicht vorenthalten. Ich werde nächstens meiner Sache so gewiß sein, daß ich in der Volkszeitung einen Preis (und zwar wähle ich dazu eine vollständige Sammlung der Autographen der Berliner Schuldirektoren) auszusetzen gedenke für ein Beispiel, wo die Methode nicht stimmt.“

Von dieser Zeit an blieb ich beständig in Verbindung mit du-Bois, und wenn auch hier nicht der Ort ist, auf die Leistungen dieses hervorragenden (Seite 40) Mathematikers einzugehen, so darf ich es doch nicht unterlassen, aus einer langjährigen Korrespondenz mit mir einzelne Stellen hervorzuheben, die für den Charakter und die Anschauungsweise meines alten Freundes charakterisch sind und mannigfache Anhaltspunkte für die Darstellung der Folgezeit bieten werden.

Nachdem er nicht ohne mein Zutun von Heidelberg nach Freiburg berufen worden, wo er mit seiner akademischen Tätigkeit recht zufrieden war, veranlaßten ihn finanzielle Gründe schon nach kurzer Zeit einem Rufe nach Tübingen zu folgen; die Wiederbesetzung seiner Stelle in Freiburg bereitete ihm viel Sorge und Ärger, und es ist charakteristisch für ihn, daß er sich mit dem Gedanken trug, den wenn auch sehr hervorragenden Mathematiker Schläffli in Bern vorzuschlagen, der schon durch sein Alter für diese Stelle wenig geeignet war, und daß er, wie er mir schrieb, seine Absicht nur aufgab, weil ihm Weierstraß dringend davon abgeraten.

Seine Briefe hatten stets etwas anregendes, häufig jedoch bizarres; so schrieb er mir aus Tübingen im Jahr 73:

„Durch Betrachtung gewisser Differentialgleichungen bin ich auf garnicht complicirte Integrale gestoßen, die ganz wie die Weierstraß'schen Reihen Functionen ohne Differentialquotienten ihrer Parameter sind. Dieselbe Eigenschaft müssen unzählige andere haben. Ich gewinne immer mehr die Überzeugung, daß die Eigenschaft, differentiirbar zu sein, eine ganz exceptionelle Güte der Functionen ist, die (Seite 41) man nur bei den algebraischen und den ähnlich organisirten findet, und die ungeheure Mehrzahl keinen Differentialquotienten hat.“

Die Berufung von Freiburg nach Tübingen brachte ihm nicht die gehoffte innere Zufriedenheit,

„Weinen Sie — schreibt er mir im Jahre 76 — im schönen Dresden eine Träne über mich im Tübinger Mist Zappelnden. In Freiburg war ich nach einem Jahr weiter, da standen mir aber auch andere Leute zur Seite, deren Mitwirkung meine Bemühungen stützte. Hier bin ich vollständig isoliert ..... kurz, während ich in Freiburg den kleinsten Gehalt unter allen deutschen Mathematikern hatte, habe ich hier die kleinste Wirksamkeit“;

„Ihre Geschichte der elliptischen Functionen^(2.8) ist mir sehr erwünscht gekommen und sehr nützlich gewesen. Es ist nicht genug zu danken, daß Jemand, der die Sache so funditus versteht wie Sie, sein (Seite 42) schriftstellerisches Talent dazu verwendet, Andere, die dem Gegenstand ihre Arbeitskraft ausschließlich zu widmen, nicht in der Lage sind, im Grunde genommen alles das bietet, was sie nur begehren können, Einsicht in das Werden und Gewordensein eines so belangreichen Theiles der Wissenschaft. Einen Punkt konnte man vielleicht hervorheben, den Sie aber nicht hervortreten lassen wollten. Es ist der unangenehme Ton Abels' Jacobi gegenüber. In meinen Augen ist trotz der Fülle tiefer Gedanken, die Abel in die Theorie hineinträgt, Jacobi doch der Bahnbrecher. Es dreht sich doch alles schließlich um die ϑ-Funktionen, sie sind das vornehmste Resultat der ganzen Periode, und ihre Erscheinung ist der Markstein einer neuen mathematischen Epoche. Doch fällt mir eben ein, daß ich in die Theorie der ϑ erst durch Ihr Buch gründlich eingeweiht worden bin, und daß es eigentlich sonderbar erscheinen muß, wenn ich Ihnen noch davon erzählen will.“

Wie wohl er nun auf immer größere Erfolge in seiner Lehrtätigkeit hinweisen kann, sehnt er sich trotzdem aus Tübingen fort, weil er in seiner Unzufriedenheit Haß gegen alles Norddeutsche zu bemerken glaubt: „ich selbst gebe mich schon längst als einen Schweizer aus.“ Er wird jetzt auch bisweilen recht bitter gegen andere; als ich ihm im Winter 81 auf seine Anfrage beuüglich der Besetzung einer zweiten mathematischen Professur in Tübingen unter anderen auch Hamburger in Vorschlag brachte, antwortete er mir ein wenig gereizt:

„Was Hamburger anlangt, so weiß ich nicht, ob ich in meinem Interesse handle, wenn ich ihn (Seite 43) vorschlage; er hat mich geärgert durch kurze schnoddrige wegwerfende Referate in den „Fortschritten“ über einige meiner Arbeiten, denen die Folge keineswegs Recht gegeben hat, die mir aber geschadet haben; ich weiß, daß Hamburger kenntnisreich ist, und ich würde viel lieber einen reifen Mann an meiner Seite haben wie einen jungen, der erst erzogen werden muß. Aber wenn der Reife kein sicherer Freund und Halt zu werden verspricht, so fürchte ich für meine Ruhe, denn Reibereien und Kampf scheint mir, Angesichts des Haufens Arbeit, den ich beständig vor mir habe, eine überflüssige Zugabe zu den unvermeindlichen Schwierigkeiten der Existenz zu sein“;

„diesem Burschen stecke ich bei nächster Gelegenheit eine Dynamitpatrone in den Leib. Das ... will von dort weg und denkt mich als Sprungbrett gebrauchen zu können“

Daß seine „Functionentheorie“ den Mathematikern ein wenig fremdartig und mystisch erscheinen würde, fühlte er selbst; so schreibt er mir am 23. Juli 82:

(Seite 44) „Ich habe Ihnen und verschiedenen Anderen kein Exemplar meines ersten Heftes der allgemeinen Functionentheorie geschickt, weil nach Absetzung der Pflichtexemplare und des Exemplars für meinen vermuthlichen Recensenten in den „Fortschritten“ ich mich Bedingungen hatte unterwerfen müssen, die mir wider den Mann gingen. Es war mir sehr schmerzlich diese Gelegenheit zur Erneuerung verschiedener Beziehungen vorbeigehen zu sehen, allein ich tröste mich damit, daß ich auch Manchem erspart habe, mir, wenn auch nur einige Schritte auf die dürre Weide der Speculation folgen zu müssen.“

Vom Jahre 83 an machte er nun verzweifelte Anstrengungen, um an eine andere Universität berufen zu werden, und als ich im folgenden Jahre wieder von Wien nach Heidelberg zurückkehrte, schrieb er mir:

... „Verehrter Freund! Ich vermuthe, daß in Heidelberg jetzt alles fest ist, und daß Sie dort schon gemietet haben. Ich hatte nicht entfernt an den Ernst Ihrer Candidatur geglaubt sondern meinte, es handle sich nur um H. Weber oder mich. Von mir ist, wie es scheint, garnicht die Rede gewesen. Ich gönne Ihnen übrigens von Herzen die Erfüllung Ihrer Wünsche, und selbst, wenn ich ernstlich in Frage gekommen wäre und erfahren hätte, daß Sie dasselbe Ziel verfolgen, so würde ich eingedenk alter Verpflichtungen schwerlich versucht haben, Ihnen den Rang abzulaufen. Der einzige Hoffnungsstern ist nun Wien, wenn Sie und die Wiener Facultät mich als Ihren Nachfolger wünschen sollten.“

(Seite 45) Zugleich teilt er mir mit, daß er jetzt die Differentialquotienten einer der Differentialgleichung {ð²u / ðx²} + {ð²u / ðy²} = 0 genügenden Funktion u auf dem Rande der Fläche untersuche;

„Weierstraß soll gesagt haben, daß die ersten Differentialquotienten  ðu/ðx, ðu/ðy auf dem Rande im Allgemeinen jeden Sinn verlieren; da nun Weierstraß keine falschen Sätze aufzustellen pflegt, so hat es mich einigermaßen verwundert zu finden, daß wenigstens bei der Kreisfläche die Differentialquotienten am Rande im allgemeinen bestimmt und endlich sind, sogar in Punkten, von denen man das Gegentheil vermuthen würde, wie z. B. in solchen Punkten, in denen der vorwärts und der rückwärts genommene Differentialquotient des auf dem Rande gegebenen gedachten u verschieden sind; doch bin ich darüber noch nicht völlig im Reinen.“

Als nun aber aus Gründen, die mit den damaligen politischen Verhältnissen zusammenhingen, auch die Aussicht auf eine Berufung nach Wien scheiterte, da richteten sich seine Augen auf den mathematischen Lehrstuhl an der technischen Hochschule in Berlin, und nachdem es ihm durch Weingarten geglückt, dorthin berufen zu werden, trat endlich Gleichgewicht und Ruhe in seinem Innern ein, und reiche produktive Arbeit zeugte von der Zufriedenheit mit seiner nunmehrigen Lage. Ich sah ihn dann nur noch zweimal in Heidelberg wieder, das letztemal beim Heidelberger (Seite 46) Jubiläum 1886; drei Jahre darauf starb er, noch nicht 60 Jahre alt.

Zu diesen hervorragenden Mathematikern gesellte sich häufig mein früherer Posener Mitschüler Hamburger, der seinen jüdisch-orthodoxen Eltern das Opfer brachte, sein Leben als Lehrer an einer jüdischen städtischen Schule hinzubringen, bis er endlich schon als alter Mann eine außerordentliche Professur an der technischen Hochschule in Berlin erhielt; er wurde nur 67 Jahre alt. Seine Arbeiten über die Zyklen in den Verzweigungspunkten algebraischer Funktionen sowie besonders seine tiefsinnigen und abschließenden Untersuchungen über die singulären Integrale der Differentialgleichungen haben ihm unter den Mathematikern einen hochgeschätzten Namen gemacht. Bescheiden, milde in der Beurteilung der Arbeiten anderer, doch nicht überschwänglich in seinem Lobe, wahr, wenn es im wissenschaftlichen Interessse galt, Fehler auch in den Arbeiten seiner Freunde aufzudecken, war er uns ein lieber und hochgeehrter Freund. Nach jahrelangem mündlichen Verkehr entspann sich zwischen uns beiden, zum Teil veranlaßt durch die mißlichen finanziellen Verhältnisse Hamburgers und meine Bemühungen, ihm zur Erlangung einer seiner Bedeutung würdigen Stellung behilflich zu sein, auch eine längere Korrespondenz privater und wissenschaftlicher Natur. Zur Charakteristik dieses wegen seiner Gutherzigkeit, Wahrheitsliebe und wissenschaftlichen Bedeutung geliebten und verehrten Freundes und Kollegen, dessen Lob mich stets erfreute, da es nicht in Redensarten bestand, sondern stets sachlich (Seite 47) begründet wurde, und dessen rücksichtslos geübter Tadel, wenn es sich darum handelte, Fehler und Irrtümer nachzuweisen, mich stets warnte und beschämte, will ich an dieser Stelle in Zuneigung und Wehmut einige Briefe veröffentlichen, die zum Teil vielleicht auch wissenschaftlich von weiterem Interesse sind:

„Berlin d. 20. Februar 1881. Verehrter Freund! Herzlichen Dank für den recht freundschaftlichen Dienst, den Sie mir in einer so außerordentlichen Angelegenheit erwiesen haben. Die Aussicht, dort anzukommen, ist, soweit sie von du-Bois abhängt, sehr gering, da ich das Unglück hatte, vor geraumer Zeit allerdings, eine Arbeit von ihm, deren Bedeutung ich nicht zu würdigen vermochte, in den „Fortschritten“ geringschätzig zu beurtheilen. .... Was Ihr Buch betrifft, so bin ich seit Kurzem mit der ersten Lectüre desselben fertig geworden, deren noch viele werden folgen müssen, wenn ich den damit überlieferten Schatz von neuen weitgehenden Principien, den mannigfaltigen, höchst originellen Methoden für ihre Anwendung und so überraschenden, die wichtigsten Fragen auf dem gesammten Gebiete der analytischen Functionen berührenden Resultaten nur einigermaßen übersichtlich ordnen und mir zu eigen machen will. Denn hier gilt so recht das Wort: erwirb es, um es zu besitzen. Als Sie zum ersten Mal den Satz von der Erhaltung der algebraischen Beziehung u.s.w. veröffentlichten, so frappirte mich die unübersehbare Tragweite desselben, und ich ahnte sofort die enorme Fruchtbarkeit an Ergebnissen. Die Reihe von schönen Arbeiten, die (Seite 48) Schlag auf Schlag einander folgten, hat die Erwartungen auf das glänzendste bestätigt. Hierbei fiel mir als eine neue Conception, die im Zusammenhang mit der vorigen einen verstärkten Impuls zu weiteren Folgerungen gab, die originelle Fassung des bekannten Abel'schen Satzes auf, daß das Integral einer algebraischen Function, wenn es algebraisch sein soll, eine rationale Function von x, y sein müsse; der einfachere und zugleich allgemeinere Inhalt, der dadurch gewonnnen war, ergab sofort einen größeren Umfang seiner Anwendung, nämlich die Erweiterung auf Integrale linearer Differentialgleichungen überhaupt. In diesem Buche aber erkennt man doch erst den ganzen reichen Organismus von Erkenntnissen, die durch die neuen schöpferischen Ideen sich aufthun, neue Probleme werden gestellt und gelöst, die Lösungen der alten theils erweitert, theils ihrer nothwendigen Form nach, auch soweit sie bekannt waren, fixiert. Weingarten sagte von Fuchs einmal „er habe mit seiner Arbeit zur Theorie der Differentialgleichungen ein gut Fäßchen angestochen“, dasselbe läßt sich treffend von Ihrer Arbeit sagen,“

„ich habe Ihren Beweis sofort wiederholter Prüfung unterzogen; das Ergebnis ist, daß ich das von (Seite 49) Ihnen beim Beweise angewandte Princip nur dann für richtig anerkennen kann, wenn folgender nach dem nämlichen Prinzip zu erweisende allgemeinere Satz richtig ist; er lautet: wenn die unendliche Potenzreihe mit rationalen Coeffizienten a₀ + a₁x + a₂x² + ... für ein irrationales x = \alpha einen Werth A annimmt, der rational oder irrational sein kann, und es stehen sämmtliche Werthe von x, welche dieser Reihe den Werth A zuertheilen, in einer solchen Beziehung zu einander, wie dieselbe zwischen Lösungen einer algebraisch irreductibeln Gleichung mit rationalen Coefficienten nicht bestehen kann, so wird der Ausdruck a₀ + a₁x + a_nxⁿ von einem bestimmten n an stets irrational sein. .....“

Aber der ausgesprochene Tadel macht ihm Skrupel; schon wenige Tage darauf schreibt er mir:

„auf Ihre erneute Darlegung hin habe ich nochmals alle in Betracht kommenden Argumente reiflich erwogen und finde mich dadurch belohnt, daß ich, nachdem ich beim ersten Anlauf mich in meinen Zweifeln bestärkt gefunden, nach dem völligen Durchdenken dieser Skrupel grade die vollkommne Überzeugung von der Unantastbarkeit Ihrer Argumente gewann. Freilich muß ich dadurch eingestehen, daß ich mit meiner Bemerkung, die zu meinem Bedauern bereits gedruckt ist, voreilig gewesen bin, und das schmeichelhafte Prädicat, womit Sie so freundlich meine wissenschaftliche Qualität bezeichnen, mehr in Ihrem Wohlwollen als in der Sache begründet ist.“

Die Richtigstellung des bereits gedruckten Referats hatte für mich kein weiteres Interesse; bei einer andern Gelegenheit schrieb mir Weierstraß:

(Seite 50) „Ich für meinen Theil würde niemals mit einem Recensenten in eine Kontroverse mich einlassen, es sei denn, daß es sich nur um eine sachliche Berichtigung von Mißverständnissen handelt.“

Doch nicht immer brauchte Hamburger mir gegenüber einen Tadel, den er ausgesprochen, so bereitwillig zurückzunehmen. Er machte mich im März 91 auf einen Fehler in meinem Lehrbuch der Differentialgleichungen aufmerksam, den ich auch sogleich als solchen anerkannte, und er tat dies offen und liebenswürdig mit den Worten:

„ ..... nun finde ich einen Fehler, den ich im Referat nicht übergehen kann, halte es aber für meine Pflicht, Ihnen vorher davon Mittheilung zu machen, damit Sie Gelegenheit haben, falls es Ihnen angemessen scheint, vorher eine Berichtigung zu veröffentlichen, auf die ich mich dann einfach beziehen kann.“

Daß ich das letztere nicht getan und Hamburger somit sein früheres Referat drucken ließ, brauche ich kaum zu bemerken.

Dies waren die Männer, mit denen ich in der Zeit meiner Lehrtätigkeit am Kadettenkorps fast täglich verkehrte; aberr vor allem war ich damals durch das Interesse beglückt, welches mir Weierstraß zuwendete, den ich häufig an freien Nachmittagen besuchen durfte, um ihm von meinen Studien zu erzählen und seinen Worten mit Pietät zu lauschen, wenn er mir aus seinen Untersuchungen in der Theorie der Abelschen Funktionen mancherlei mitteilte. In diesen Jahren sowie später (Seite 51) noch am Anfange meiner Universitätstätigkeit in Greifswald, überließ er mir große Teile seiner Manuskripte über die Umkehrung der hyperelliptischen Integrale und die ϑ-Funktionen mehrerer Variabeln zur Einsicht. Sehr bedauert habe ich es stets, daß ich, als sich allmählich seine Untersuchungen der allgemeinen Funktionentheorie zuwandten, in die er mit genialer schöpferischer Kraft eingriff, eine Vorlesung darüber bei ihm zu hören, nie in der Lage war. Mit großer Freude bemerkte ich sein Interesse für meine erste Arbeit, die ich, auf Grund der berühmten Abhandlung von Hermite, über die Transformation und die Modulargleichungen der hyperelliptischen Funktionen erste Ordnung^(2.9) bei ihm vorlegte; unsere Unterhaltung drehte sich zu jener Zeit meist noch um Fragen aus der Theorie der Abelschen Transzendenten, wandte sich häufig aber auch allgemeinereen funktionentheoretischen Betrachtungen zu. So beschäftigte er sich schon damals mit der Einführung seiner Elementarteiler für die Produktentwicklung analytischer Funktionen; als ich einmal Kronecker bei ihm traf, und auf seine Frage, womit ich mich jetzt beschäftigte, ihm mitteilte, daß ich die Eisensteinschen Arbeiten über unendliche Produkte gelesen, aber vieles unstreng und sogar falsch gefunden habe, da wandte er sich an Kronecker, mit dem er offenbar unmittelbar vorher über seine Darstellung der von der Reihenfolge der Faktoren unabhängigen Produkte gesprochen hatte, mit den Worten: „Herr Dr. K. hält auch die Eisensteinschen Deduktionen, um die es sich eben handelt, für sehr angreifbar,“ und nun begann zwischen den beiden Meistern die (Seite 52) Diskussion aufs neue, der ich andächtig als stiller Zuhörer und Bewunderer beiwohnte. Jeder Besuch bei diesem wahrhaft großen Mathematiker bereicherte meine Kenntnisse mit Neuem und Ungeahntem in meiner Wissenschaft, aber auch manche ergötzliche Episode ist mir von diesen Besuchen in Erinnerung geblieben: Ich hatte einige Jahre früher als zweisemestriger Student die von Steiner angekündigte Vorlesung über Kegelschnitte hören wollen, zu der sich etwa 6 bis 8 Zuhörer im Auditorium eingefunden hatten; bei seinem Eintritt musterte uns der schon durch seine äußere Erscheinung Ehrfurcht gebietende große Geometer, fragte uns, ob wir wirklich ernsthaft bei ihm hören wollten, und als wir dies bejahten, zog er bedächtig sein großes rotes Taschentuch heraus, räusperte sich längere Zeit, erklärte aber endlich, es sei doch wohl besser, wenn wir die Sache aus Büchern lernten und verschwand. So hatte ich mehrere Jahre keine Gelegenheit Steiner wiederzusehen. Als ich eines Nachmittags bei Weierstraß war und mit ihm an seinem Arbeitstisch sitzend gemeinsam die Einleitung zu der Fischerschen Bearbeitung der Untersuchungen von Puiseux las, trat, als wir eben zu der Stelle der dort willkührlich gezeichneten Charakteristik gelangt waren, Steiner ins Zimmer, den Weierstraß, nachdem er mich ihm vorgestellt hatte, bat, sich ein wenig zu gedulden, bis wir den Abschnitt zu Ende gelesen. Steiner trat hinter uns und blickte über unsere Köpfe weg in das Buch, das vor uns lag. Als Weierstraß die Seite umgeschlagen, auf welcher die Charakteristik verzeichnet, streckte Steiner (Seite 53) seine große Hand zwischen uns und drehte das Blatt wieder zurück; als sich dies zum zweitenmal unmitttelbar darauf wiederholte, wandte sich Weierstraß, über die Störung ärgerlich, um und fragte, was er denn wolle. Steiner antwortete, er möchte wissen, was das für eine Figur sei, und als Weierstraß lächelnd erwiderte, es sei eine beliebig gezeichnete Abgrenzung eines Raumteils, brach Steiner in etwas gereiztem Tone los „bei Euch Analytikern ist alles beliebig und willkürlich, für uns Geometer ist nichts willkürlich, jedes Gebilde befolgt seine Gesetze.“ Mir blieb nur übrig, bei dem folgenden Wortgeplänkel die beiden Heroen der Analysis und Geometrie in stiller Bewunderung anzustaunen.

So vergingen meine ersten Jahre nach vollendetem Studium in ernster angestrengter Arbeit in engem Zusammenleben mit Fuchs, der sich schon Ende 63 mit Riemanns Arbeit über die Differentialgleichung der hypergeometrischen Reihe zu beschäftigen begann. Borchardt, dem verdienstvollen Redakteur des Crelleschen Journals und scharfsinnigen, überaus gelehrten Mathematiker, den wir zu alledem als den einstmaligen intimen Freund Jacobis hochachteten, blieben wir wegen seiner steifen Förmlichkeit ziemlich fremd und kamen meist nur dann mit ihm in Verbindung, wenn wir ihn um die Aufnahme einer Arbeit in sein Journal angingen. Aber auch als Redakteur war er äußerst penibel, und wir bedurften häufig der Empfehlung von Weierstraß oder Kummer, wenn er unsern Arbeiten eine Stelle in seinem Journal einräumen sollte, zumal da er der damals einsetzenden Strömung (Seite 54) moderner mathematischer Anschauungen nicht besonders zugetan war; von den Berliner Mathematikern war es nur Weierstraß, der sehr bald erkannte, daß die von ihm für hyperelliptische Funktionen entwickelten Resultate und die für allgemeine Abelsche Funktionen gewonnenen Sätze durch Riemanns Untersuchungen überholt würden. Auch wir jüngeren Mathematiker hatten damals sämtlich das Gefühl, als ob die Riemannschen Anschauungen und Methoden nicht mehr der strengen Mathematik der Euler, Lagrange, Gauß, Jacobi, Dirichlet u. a. angehörten — wie dies ja stets der Fall zu sein pflegt, wenn eine neue große Idee in die Wissenschaft eingreift, welche erst Zeit braucht, um in den Köpfen der lebenden Generation verarbeitet zu werden. So wurden die Leistungen der Göttinger Schule von uns, zum Teil wenigstens, nicht so geschätzt, als es ihrer großen Bedeutung zukam, und wir gaben ihnen häufig nicht sogleich die Stelle, welche die Wissenschaft ihnen sehr bald anwies.

Im übrigen verlief unser arbeitsvolles Leben ruhig und ohne Zwischenfälle und erhielt nur Freude und Anregung von außen durch politische Diskussion und wissenschaftliche Dispute; die Unzufriedenheit einiger aus unserm Kreise mit der schulmeisterlichen Tätigkeit, die mir persönlich recht gut behagte, gab der Unterhaltung Heiterkeit und Würze. Fuchs mußte der vielen Privatstunden wegen auch die Ferien in Berlin zubringen, während ich, nachdem ich wegen eines vorübergehenden Magenleidens beim Militär der Ersatzreserve überwiesen worden, regelmäßig in den freien Wochen meine Eltern besuchte (Seite 55) und dank ihrer liebevollen Pflege bald wieder gesundete; der häufige Verkehr mit einem mir sehr sympathischen Realschulprofessor Magener, einem alten Jacobischen Schüler, der sich auch durch einige Arbeiten über Fußpunktenflächen bekannt gemacht, ließ mir auch dort noch hinreichende Zeit zu mathematischen Studien. Als ich später auch von Heidelberg aus zum Besuche meiner Eltern nach Posen kam, waren mir die Erzählungen Mageners aus seiner Posener Gymnasialzeit besonders interessant. Er hatte mit Kuno Fischer, dem mir befreundeten Heidelberger Kollegen, die oberen Klassen des Gymnasiums besucht und mit ihm zugleich das Maturitätsexamen gemacht; er schilderte mir ihn gern in seiner Doppelnatur, die ihm bis in sein spätes Alter zu eigen geblieben. Wie er als Primaner in einem Boot eine kleine Wartheinsel umkreisend in kindlich-naiver Weise unbekümmert um mißgünstige Beobachter der schönen Fischerstochter in Liebesliedern gehuldigt, ohne je an der Insel zu landen, so hat er später im mündlichen Verkehr in treffend geprägten Urteilen bedeutenden Männern der Wissenschaft und Politik gehuldigt oder ihre Anschauungen und Handlungen getadelt und mit der Offenheit eines Kindes unbekümmert um seine Person diese Urteile wiederholt der breiten Öffentlichkeit preisgegeben — und wie er damals als Primaner in den Zwischenstunden bisweilen eine pathetische Rede an seine Mitschüler gerichtet und bei dem leisesten Lächeln eines der Zuhörer sich im Zorn an diesem zu vergreifen suchte, so kannte der ausgezeichnete Philosoph und unübertroffene Lehrer (Seite 56) auch später keine Grenze in Wort und Tat, wenn er glaubte, daß seiner persönlichen Würde oder wissenschaftlichen Meisterschaft Abbruch geschah.

Da ich bei der großen Zahl meiner unversogten Geschwister von meinen Eltern nicht die Mittel verlangen durfte, um mich an der Berliner Universität zu habilitieren und ganz der wissenschaftlichen Arbeit widmen zu können, so hatte ich mich schon mit dem Gedanken vertraut gemacht, für immer am Kadettenkorps oder an einem Berliner Gymnasium meine pädagogische Tätigkeit auszuüben, als ich um die Weihnachtszeit 63 von dem Unterstaatssekretär Olshausen die schriftliche Anfrage erhielt, ob ich bereit sei, Ostern 64 eine etatmäßige außerordentliche Professur an der Universität Greiswald anzunehmen; mein Lehrer Weierstraß habe mich für diese neu kreierte Stelle der Fakultät empfohlen. War der in Aussicht gestellte Gehalt im Vergleich zu den freilich unsicheren Einkünften in Berlin auch ziemlich gering, so zögerte ich doch keinen Augenblick, auf das für mich ehrenvolle Anerbieten einzugehen und erhielt auch im November 63 von dem Unterrichtsminister v. Mühler die Anzeige von meiner Ernennung, welche mit den damals üblichen Worten schloß: „überhaupt aber sich so zu betragen, wie es einem treuen und geschickten Königlichen Diener und Professor wohl ansteht und gebührt.“ Freilich konnte ich dabei ein unangenehmes Gefühl Fuchs gegenüber, zu dessen wissenschaftlicher Bedeutung ich stets hinaufgesehen, nicht unterdrücken, und es fiel mir die Trennung von ihm, mit dem (Seite 57) ich mit kurzen Unterbrechungen fast 10 Jahre zusammengelebt, sehr schwer. Vom Kadettenkorps, an dem ich noch als Hilfslehrer fungierte, wurde ich nur ungern entlassen, und das von dem General v. Ollech ausgestellte Zeugnis:

„.... er hat sich in dieser Zeit durch eine vortreffliche Methode seines Unterrichts in der Mathematik und Physik, durch strenge Handhabung der Disciplin und durch eine gediegene wissenschaftliche Bildung ausgezeichnet. Sein Unterricht war stets von den besten Erfolgen begleitet. Ohne seine Berufung als Professor nach Greifswald würde das Cadettencorps Herrn Dr. K. gern zur festen Anstellung als Lehrer den höheren Behörden empfohlen haben.“

Zum Abschied erhielt ich noch von Weierstraß, dem ich eine neue Arbeit über Abelsche Funktionen^(2.10) für das Crellesche Journal eingereicht hatte, die Aufforderung, ihn zu besuchen und ihm „meine sämmtlichen Ausarbeitungen über Abelsche Functionen mitzubringen, damit er beurtheilen könne, welche Materialien mit weiterhin zu Gebote stünden.“

Text: Leo Koenigsberger, 1919
Anmerkungen und Personenregister: Gabriele Dörflinger, 2004-2014

Letzte Änderung: Mai 2014     Gabriele Dörflinger   Kontakt

Zur Inhaltsübersicht     Historia Mathematica     Homo Heidelbergensis     Mein Leben / Leo Koenigsberger