18.

Akademie der Wissenschaften Werkausgabe Nicolaus Cusanus

Andrea Bregno (1418-1506): Grab von Nicolaus Cusanus in der Kirche San Pietro in Vincoli in Rom

Karlsplatz — Univ.-Platz

Zu den Langzeitaufgaben der Akademie gehörte die kritische Neuausgabe der Werke Nicolaus Cusanus (1401-1464). Dieser Theologe und Philosoph an der Schwelle der Neuzeit verwendete geometrische Grenzwertbetrachtungen, um die Eigenschaften Gottes zu erklären.

Die Herausgabe der Cusanus-Werke begann 1927/28 und wurde im Jahr 2005 abgeschlossen. Raymond Klibansky (1905-2005) — damals noch als Student unter dem Initiator Ernst Hoffmann tätig — erlebte gerade noch die Vollendung dieses Opus Magnum.

Literatur:

Beierwaltes, Werner:

Die Cusanus-Edition der Heidelberger Akademie der Wissenschaften. Heidelberg, 2011.

Dörflinger, Gabriele (Hrsg.):

Die Cusanus-Edition der Heidelberger Akademie der Wissenschaften : Jahresberichte 1927 bis 1959 aus dem Jahresheft der Heidelberger Akademie.

Nicolaus Cusanus schrieb sich Ende 1415 an der Universität Heidelberg ein. Er verließ Heidelberg im Jahr 1417. Nach weiteren Studien in Padua wurde er 1430 zum Priester geweiht. Er nahm 1432 am Konzil in Basel teil, wo er (vergeblich) eine Kalenderreform forderte. Er wurde 1448 Kardinal, 1450 Bischof von Brixen und wirkte als päpstlicher Legat.

In den Kapiteln 11 bis 17 seines zentralen Werkes De docta ignorantia beschäftigte sich Cusanus mit geometrischen Grenzwertüberlegungen, der Art

• je stärker der Durchmesser eines Kreises vergrößert wird, desto geringer ist die Krümmung eines Kreisssegments; der unendlichgroße Kreis ist somit mit einer Geraden identisch,
• wenn die Hypothenuse eines Dreiecks verlängert wird, werden die Hypothenusenwinkel immer kleiner und die beiden Schenkel nähern sich immer mehr der Hypothenuse; bei einer unendlichgroßen Hypothenuse fallen alle drei Seiten des Dreiecks aufeinander und das Dreieck ist mit den drei Geraden identisch.

So schrieb er im 13. Kapitel (Von den möglichen Veränderungen (de passionibus) der größten und unendlichen Linie):

„Ich sage also: Gäbe es eine unendliche Linie, so wäre sie ein Dreieck, Kreis und Kugel; ebenso, gäbe es eine unendliche Kugel, so wäre sie Dreieck, Kreis und Linie; das gleiche gilt vom unendlichen Dreieck und Kreise.

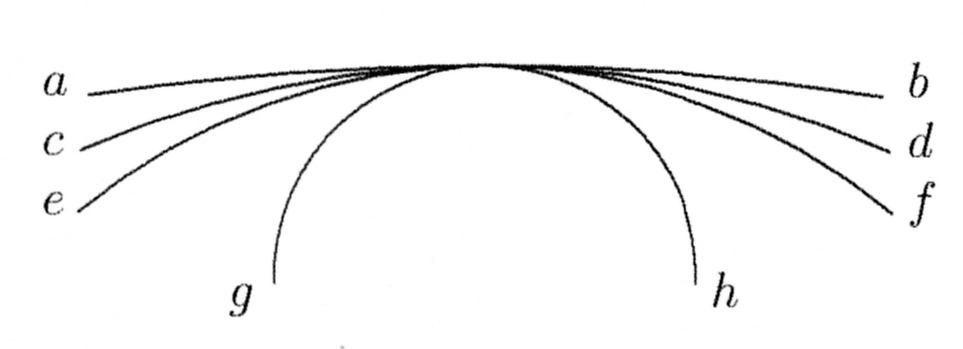Fürs erste erhellt, dass die unendliche Linie eine gerade ist. Denn der Durchmesser eines Kreises ist eine gerade Linie, die Peripherie eine krumme, größer als der Durchmesser. Wenn nun dieses krumme Linie kleiner wird, je größer der Kreis ist, so ist die Peripherie des größtmöglichsten Kreises gar nicht krumm, folglich ganz gerade; es koinzidiert also das Kleinste mit dem Größten, wie aus der hier stehenden Figur erhellt.“

„Denkt man sich den einen der drei Winkel [des Dreiecks] bis zu 2 R[echten Winkeln] erweitert, so jedoch, dass das Dreieck bleibt, so fällt das Dreieck zu einer Linie zusammen.“

Dt. Übersetzung von Franz Anton Scharpff

Letzte Änderung: Oktober 2017     Gabriele Dörflinger   Kontakt

Zur Inhaltsübersicht     Historia Mathematica Heidelbergensis     Homo Heidelbergensis