 |
Beiträge Moritz Cantors zum
Naturhistorisch-Medizinischen Verein zu Heidelberg
|
Moritz Cantor zählte zu den Gründungsmitgliedern des
1856 gegründeten
 Naturhistorisch-medicinischen Vereins.
In den Verhandlungen des Vereins sind zwischen 1856
und 1863 mehrere Vorträge Moritz Cantors
dokumentiert.
Naturhistorisch-medicinischen Vereins.
In den Verhandlungen des Vereins sind zwischen 1856
und 1863 mehrere Vorträge Moritz Cantors
dokumentiert.
Band 1 — Seite 5
4. Vortrag des Herrn Dr.
Cantor „über Porismen“, am 21. Nov. 1856.
Diese mathematisch-historische Untersuchung sollte
hauptsächlich zeigen, wie alle Divinatoren der Porismen des Euclid
immer nur den Inhalt in ihnen vermutheten, mit dem sie selbst sich
meistens beschäftigten. Diesen Nachweis zu führen, wurden zuerst die
Stellen des Pappus, Diophant, Proclus mitgetheilt, auf die jene
Divinatoren sich stützten und dann eine kritische Zusammenstellung der
Hauptansichten gegeben. Den Schluss bildete die Conjectur, es dürfte
ein besseres Verständniss der Porismen erzielt werden, wenn man die
Interpretation nicht vom geometrischen Standpunkte, sondern von dem
der Analysis aus versuche. Dann aber lasse sich folgende Analogie
neuerer und älterer Untersuchungen behaupten: Eigenschaften einer
Funktion finden, gibt das Theorem an, Werthe der Funktion bei
gegebenem Argumente leitet das Problem ab; endlich aus
Eigenschaften auf die Art der Funktion schliessen, lehrt das Porisma.
—
Anmerkung:
Ausführlicher ist das Thema im Aufsatz
 Ueber die
Porismen des Euclid und deren Divinatoren abgehandelt, der im
2. Band der Literaturzeitung der Zeitschrift für Mathematik und
Physik 1857 erschienen ist.
Ueber die
Porismen des Euclid und deren Divinatoren abgehandelt, der im
2. Band der Literaturzeitung der Zeitschrift für Mathematik und
Physik 1857 erschienen ist.
(Dörflinger, Universitätsbibliothek Heidelberg, 2011)
Band 1 — Seite 164-165
59. Vortrag des Herrn Dr. Cantor über die
Mathematik des Pythagoras am 29. November
1858.
Durch einen Abriss der Lebensbeschreibung des Pythagoras wurde
nachgewiesen, wie die mathematischen Kenntnisse desselben einen
doppelten Ursprung haben, welchen sie auch durch
Verschiedenheit des Inhaltes deutlich erkennen lassen. Aus Aegypten
stammen die geometrischen Kenntnisse, aus Babylon Alles, was auf
Zahlen sich bezieht.
Die Bedeutung der Geometrie des Pythagoras liegt nicht bloss in den
Sätzen, welche freilich an sich schon wichtig genug sind; sie liegt
ganz besonders in der formellen Methode, derjenigen
Methode, welche unter dem Namen Synthesis verbreitet ist, und
welche eine ähnlich kategetische Ausdrucksweise besass, wie sie in
allen Lehren des Pythagoras sich vorfindet.
Inhalt der geometrischen Sätze war die Theorie der Paralell-Linien
und daran anknüpfend der Verwandlung der Figuren. Ferner
Untersuchungen über regelmässige Polygone und Polyeder, wobei
auch schon die Sternpolygone in Betracht gezogen wurden. Es ist
nicht unwichtig, dass letzterer Gegenstand auch bei Boethius wieder
auftritt. Dadurch tritt die von dem Vortragenden bei verschiedener
Gelegenheit verfochtene These von der Autorität des Boethius für die
Einführung der Ziffern durch Pythagoras in ein neues Licht. Und
ähnlicherweise controlirt die Darstellung der geometrischen
Methoden des Phythagoras die Ansichten, welche der Vortragende
früher über die Porismen des Euclid aufgestellt hatte.
In Bezug auf die Zahlenlehre mussten zunächst die neuesten
Untersuchungen angedeutet werden, welche den indirect
babylonischen Ursprung der Zahlzeichen unabweisbar erscheinen
lassen. Es
wurde alsdann gezeigt, wie China (vielleicht das ursprüngliche
Vaterland der Ziffern) schon in vorpythagorischer Zeit den Satz kannte
dass Seiten von der Länge 3, 4, 5 ein rechtwinkliges Dreieck
bilden; dass ferner zahlentheoretische Untersuchungen im Oriente zu
den verbreitetsten gehören. Daher durfte die Hypothese aufgestellt
werden : Pythagoras habe sich mit derjenigen unbestimmten Aufgabe
beschäftigt, welche in modernen Zeichen
x² + y² =
z²
heissen würde; er habe eingesehen, dass die Zahlen 3, 4, 5 unter
Anderen ihr genügen, und dadurch habe der chinesische Satz, der sich
auf dieselben Zahlen bezog, Interesse für ihn gewonnen. Er habe ihn zu
beweisen gesucht, und da dieser Beweis, wie früher gezeigt, nur
geometrisch sein konnte, so habe er den Satz entdeckt, welcher seinen
Namen führt. Diese Hypothese allein erklärt Alles, was bisher noch
dunkel oder widersprechend: schien, und
namentlich in Röth's sonst vortrefflicher Schilderung
des Pythagoras und seiner Mathematik noch sehr mangelhaft ist.
Besonders einleuchtend wird es jetzt, wie der Satz vom
rechtwinkligen Dreiecke weit weniger zu geometrischen als zu
zahlentheoretischen Consequenzen führte, wie aus ihm der Begriff der
Irrationalzahlen fliessen musste u. s. w.
Die Auflösung der Gleichung
x² + y² = z²
scheint in der Weise geliefert worden zu sein, dass man daraus
x² = (z+y) · (z-y)
folgerte und alsdann für z+y und z-y
ähnliche Flächenzahlen einsetzte , etwa
z + y
= α · β²,
z - y = α · γ²,
woraus die Werthe
x = α · β · γ
y = α/2 (β² - γ²)
z = α/2 (β² +
γ²)
folgen. Aus diesen Werthen ergeben sich wenigstens am Einfachsten
die zwei Auflösungen, welche die Alten schon dem Pythagoras-und
dem Plato zuschrieben; aus ihnen folgt ebenso auch die Bedeutung,
welche das Hetoromekeis genannte Product n(n + 1) bei
diesen Mathematikern besass.
Band 2 — Seite 67-68
30. Vortrag des Herrn Dr. Cantor „über die
Lebenszeit des Zenodorus“, am 26. October 1860.
Herr Professor Nokk in Freiburg veröffentlichte als Programm
des dortigen Lyceums eine Uebersetzung der isoperimetrischen
Untersuchungen des Zenodorus, wozu er den Text den gleichlautenden
Auszügen entnahm, wie sie bei Theon von Alexandrien und bei Pappus
sich finden. Er knüpfte daran Untersuchungen über die Lebenszeit des
Zenodorus, und bewies, dass derselbe des Archimedes Schriften
angeführt habe, also jedenfalls später als 250 v. C. gelebt haben
müsse. Der Vortragende suchte nun die eigentliche
Lebenszeit jenes griechischen Mathematikers noch näher zu bestimmen,
welche wegen der Wichtigkeit seiner Forschungen von Interesse ist,
insofern es bedeutsam erscheinen muss, wann so tiefe
Untersuchungen zuerst geführt wurden. Die Historiker waren seit
Ramus
übereingekommen, in Zenodorus einen Schüler des Oenopides von
Chios zu sehen, und setzten ihn mit geringen Verschiedenheiten von
552 - 452 v. C. Wenigstens finden sich diese Angaben bei Blancanus,
Heilbronner, Montucla u. A. Etwas später setzte ihn Baldi, nämlich in's
Jahr 398 v. C., indem er ihn Schüler des Andron und Anhänger der
Lehre des Oenopides nennt. Vossius spricht zwar von Oenopides, ohne
jedoch den Namen des Zenodorus zu erwähnen. Diese Angaben, welche
sämmtlich schon durch die Beweisführung des Herrn Nokk als unhaltbar
sich ergeben, stützen sich sämmtlich auf eine Stelle des Proclus,
welche im Urtexte der Basler Ausgabe folgendermassen lautet:
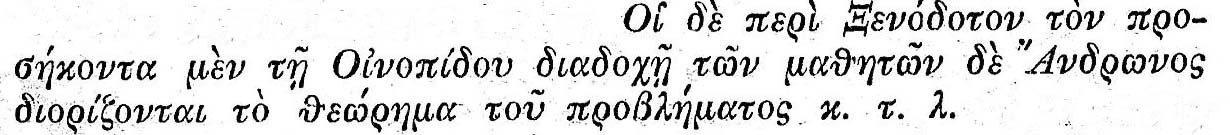 Der Vortragende schlug dazu zwei andere Lesarten vor:
τòν μαϑητην
und
Zηνóδoτoν. Für die erstere spricht
schon der bessere Sinn, für die zweite besonders die Uebersetzung des
Barocius, welcher bekanntlich ausser dem Basier Drucke noch mehrere
bessere Manuscripte zu Grunde liegen; dann auch die schon von Herrn
Nokk angeführte Stelle der Bibliotheca Graeca des Fabricius (tom. IV.
pag. 84). Die Veränderung von Zenodotus in Zenodorus macht aber
keine Schwierigkeit, indem ganz ebenso Diodorus und Diodotus
synonim gebraucht werden. Damit würde also Zenodorus in
bestimmten Fragen der Schule des Oenopides angehören; sein
unmittelbarer Lehrer wäre aber Andron, auf dessen Zeit Alles ankäme.
Der einzige Mathematiker dieses Namens wurde aber in der von J.
Capitolinus verfassten Biographie des Kaisers M. Antoninus
Philosophus aufgefunden, wo Andron als Lehrer des Kaisers in den
mathematischen Disciplinen genannt wird. Nach Zedler
(Universallexicon Bd. II. S. 208) soll Andron aus Catanea auf Sicilien
gebürtig sein. Er muss am Anfange des 2. Jahrhunderts n. C. gelebt
haben und somit wäre Zenodorus ein etwas älterer Zeitgenosse des
Ptolemaeus, was für die Beiziehung im Commentare des Almagest
gleichfalls stimmen würde. Dass von jenem Andron Nichts weiter
bekannt ist, als dass er Lehrer des Kaisers Antoninus war, kann fast als
negative Unterstützung angesehen werden, indem er späteren
Mathematikern unbekannt, der frühen Nachkommenschaft (Proclus
schrieb etwa 100 Jahre nach Capitolinus) als Lehrer jenes Kaisers noch
erinnerlich genug war. Was endlich den Einwurf
betrifft, ob der bei Proclus angeführte Gegenstand des Zenodorus
würdig gewesen, und ob nicht daraus hervorgebe, dass der genannte
Mathematiker von dem Verfasser der isoperimetrischen Untersuchungen
verschieden sei, so ist einmal zu bedenken, dass Proclus, bei welchem
die Stelle sich findet, selbst weit weniger Mathematiker als Philosoph
war, und desshalb einen andern Maassstab des Werthes anlegen
mochte, dann aber auch, dass in der That die
philosophische Begründung der Mathematik ihre Rechte hat und von
den tüchtigsten Mathematikern bis in die neueste Zeit (Legendre:
Theorie der Parallelen, Gauss: Theorie des Imaginären u. s.w.) gepflegt
wurde.
Der Vortragende schlug dazu zwei andere Lesarten vor:
τòν μαϑητην
und
Zηνóδoτoν. Für die erstere spricht
schon der bessere Sinn, für die zweite besonders die Uebersetzung des
Barocius, welcher bekanntlich ausser dem Basier Drucke noch mehrere
bessere Manuscripte zu Grunde liegen; dann auch die schon von Herrn
Nokk angeführte Stelle der Bibliotheca Graeca des Fabricius (tom. IV.
pag. 84). Die Veränderung von Zenodotus in Zenodorus macht aber
keine Schwierigkeit, indem ganz ebenso Diodorus und Diodotus
synonim gebraucht werden. Damit würde also Zenodorus in
bestimmten Fragen der Schule des Oenopides angehören; sein
unmittelbarer Lehrer wäre aber Andron, auf dessen Zeit Alles ankäme.
Der einzige Mathematiker dieses Namens wurde aber in der von J.
Capitolinus verfassten Biographie des Kaisers M. Antoninus
Philosophus aufgefunden, wo Andron als Lehrer des Kaisers in den
mathematischen Disciplinen genannt wird. Nach Zedler
(Universallexicon Bd. II. S. 208) soll Andron aus Catanea auf Sicilien
gebürtig sein. Er muss am Anfange des 2. Jahrhunderts n. C. gelebt
haben und somit wäre Zenodorus ein etwas älterer Zeitgenosse des
Ptolemaeus, was für die Beiziehung im Commentare des Almagest
gleichfalls stimmen würde. Dass von jenem Andron Nichts weiter
bekannt ist, als dass er Lehrer des Kaisers Antoninus war, kann fast als
negative Unterstützung angesehen werden, indem er späteren
Mathematikern unbekannt, der frühen Nachkommenschaft (Proclus
schrieb etwa 100 Jahre nach Capitolinus) als Lehrer jenes Kaisers noch
erinnerlich genug war. Was endlich den Einwurf
betrifft, ob der bei Proclus angeführte Gegenstand des Zenodorus
würdig gewesen, und ob nicht daraus hervorgebe, dass der genannte
Mathematiker von dem Verfasser der isoperimetrischen Untersuchungen
verschieden sei, so ist einmal zu bedenken, dass Proclus, bei welchem
die Stelle sich findet, selbst weit weniger Mathematiker als Philosoph
war, und desshalb einen andern Maassstab des Werthes anlegen
mochte, dann aber auch, dass in der That die
philosophische Begründung der Mathematik ihre Rechte hat und von
den tüchtigsten Mathematikern bis in die neueste Zeit (Legendre:
Theorie der Parallelen, Gauss: Theorie des Imaginären u. s.w.) gepflegt
wurde.
Band 3 — Seite 5-6
3. Vortrag des Herrn Dr. Cantor „über
Zahlzeichen
und Rechenmethoden der Araber“,
am 19. Dezember 1862.
(Das Manuscript wurde am 15. März 1863
eingereicht.)
In einer kurzen Einleitung zeigte der Vortragende, worauf es ihm
wesentlich ankomme. Es handle sich wiederholt um die
Geometrie des Boethius und den in derselben enthaltenen Abacus mit
eigentümlichen Zahlzeichen. Man habe von gegnerischer Seite diesen
Abacus eine Interpolation Gerberts genannt, der selbst aus
arabischen Quellen geschöpft habe. Der Vortragende hat nun den heute
nicht zur Sprache bringenden Beweis geliefert, 1) dass jener
Abacus mit seinen Zeichen wirklich dem Boethius angehöre; 2) dass er
keinenfalls von Gerbert herrühre. Kann nun noch ferner
gezeigt werden 3) dass der betreffende Abacus sicherlich nicht
arabischen Ursprunges sein könne, so ist der Gegenbeweis wider die
angedeutete Meinung in einer Vollständigkeit geliefert, wie er nur
immer verlangt werden kann.
Dieser letzte Theil des Beweises bildete den Gegenstand des heutigen
Vertrages. Es wurde gezeigt, wie die mathematische Bildung der Araber
weit späteren Datums ist, als man anzunehmen geneigt ist, wie die
Quelle dieser Kenntnisse eine doppelte war, theils aus Indien, theils aus
Griechenland entstammend. Es wurde daraus gefolgert, dass es nicht
unmöglich sei, dass ursprünglich Griechisches, oder doch wenigstens
den Griechen Bekanntes bei den Arabern sich ähnlich weiter entwickelt
habe, wie bei den Römern und den mittelalterlichen Schriftstellern, ohne
dass diese letzteren es gerade den Arabern entlehnen mussten. So
rechtfertigte sich das Auftreten der sogenannten Apices bei Boethius
und der fast ganz übereinstimmenden Gobarziffern. Dass eine
Entlehnung hier nicht stattfinden konnte, wurde durch die
Rechenmethoden ausser
Zweifel gesetzt, welche an und mit jenen Ziffern bei beiden
Schriftstellerkreisen geübt wurden. Der Vortragende setzte zu diesem
Zwecke die von ihm sogenannte complementäre Division des Boethius
aus einander und zeigte, dass dieselbe sich weit in's Mittelalter hinein
fortlebte, bei den Arabern dagegen nicht bekannt war. Diese bedienten
sich vielmehr der wissenschaftlich weit niedriger
stehenden Divisionsmethode, die heute noch dem täglichen Gebrauche
dient. Zur Begründung seiner Darstellung des arabischen Rechnens
benutzte der Vortragende 1) eine Uebersetzung der Arithmetik des
Mohammed ben Musa wahrscheinlich von Atelhart von Bath
herrührend; 2) eine Bearbeitung derselben Schrift von Johann von
Sevilla; 3) die Essenz der Rechenkunst von Beha-Eddin.
Ausserdem berief er sich noch auf die Algorithmiker des 13.
Jahrhunderts, namentlich auf den geistreichen und gelehrten Johann von
Sacrobosco, dessen durch Haliwell herausgegebene ars numerandi er in
einem noch nicht genauer bestimmten Manuscript der Grossh.
Darmstädter Hofbibliothek wieder entdeckt zu haben glaubt.
Weitere Untersuchung dieser letzteren Angabe wurde vorbehalten.
Ausführlichere Mittheilung der ganzen Untersuchung, auch der in
diesem Vortrage nur citirten Beweise finden sich in den demnächst der
Presse vorlassenden Buche des Vortragenden: „Mathematische Beiträge
zum Kulturleben der Völker.“
Band 3 — Seite 61-62
12. Vortrag des Herrn Dr. Cantor „über die
Kenntnisse der Griechen in der Zahlantheorie“, am 24.
April 1863.
(Das Manuscript wurde am selben Tage eingeliefert.)
Nachdem der Vortragende den Unterschied angedeutet hatte,
welcher zwischen der Arithmetik der Griechen und
der der neueren Mathematiker existirt, indem jene unserer modernen
Zahlentheorie entspricht, schilderte er in Kürze die Schriftsteller,
welche uns arithmetische Werke hinterlassen haben. Euklides,
Archimedas, Apollonius, Nikomachus, Theon von Smyrna, Jamblichus,
Diophantus wurden hauptsächlich erwähnt; neben diesen auch
Pythagoras, Thymaridas, Plato. — Der Ursprung der Arithmetik
wurzelt in durch die Notwendigkeit des Geschäftsverkehrs
hervorgerufener Gewandtheit mit Zahlen umzugehen. Der
Entstehungsort ist Babylon. Dorthin verweisen die Analogien,
besonders die sogenannte harmonische Analogie oder Proportion, dahin
auch die zahlensymbolisch gleiche Benutzung der Zahlen 36 und 40 bei
Chinesen und
Griechen, dahin der zahlentheoretische Ursprung des pythagoräischen
Lehrsatzes, welchen der Vortragende schon früher einmal zu
schildern Gelegenheit nahm. Aus den Proportionen entstanden nämlich
die Progressionen, wovon Euklides und Archimedes ausführlich
handeln, während Plato's Timäus als Quelle für die Betrachtungen über
stetige geometrische Proportionen dient. Die arithmetische Reihe
und deren Summirung führte zu Dreieckszahlen, zu Quadratzahlen und
heteromeken Zahlen, die Summirung der Quadratzahlen zum
pythagoräischen Lehrsatz. Von diesem selbst aus gelangte man zur
Kenntniss der Jurationalzahlen, und namentlich zwei Dreiecke, bei
welchen je 2 Seiten rational sind, die dritte irrational ist, spielen bei
Plato, bei Aristoteles und bei Euklides eine wichtige Rolle.
Ausser den Quadratzahlen und den heteromeken Zahlen
beschäftigte die griechische Arithmetik sich noch mit Flächenzahlen im
Allgemeinen, sowie mit Körperzahlen. Flächenzahlen (resp.
Körperzahlen) im engeren Sinne nannte man die Producte von 2 (resp.
3) einfachen Faktoren. Die Untersuchung wandte sich nun auf solche
einfache Faktoren oder Primzahlen, welche Eratosthenes bereits durch
die Methode des Aussiebens zu entdecken lehrte. Zur Zerlegung in
Faktoren selbst diente die Einmaleinstabelle, welche dadurch ein
integrirender Bestandteil arithmetischer Schriften wurde. Die
Summirung der Faktoren vermittelte die
Untersuchungen über vollkommene Zahlen und über befreundete
Zahlen. Dieses der Inhalt der eigentlich zahlentheoretischen Kenntnisse
der Griechen. Thymaridas und Diophantus schlugen eine mehr
algebraische
Richtung ein.
Quelle:
Verhandlungen des naturhistorisch-medicinischen Vereins zu Heidelberg
Letzte Änderung: Mai 2014 Gabriele Dörflinger
 Kontakt
Kontakt
Zur Inhaltsübersicht
 Historia Mathematica
Historia Mathematica
 Homo Heidelbergensis
Homo Heidelbergensis
 Heidelberger Texte zur Mathematikgeschichte
Heidelberger Texte zur Mathematikgeschichte


![]() Ueber die
Porismen des Euclid und deren Divinatoren abgehandelt, der im
2. Band der Literaturzeitung der Zeitschrift für Mathematik und
Physik 1857 erschienen ist.
Ueber die
Porismen des Euclid und deren Divinatoren abgehandelt, der im
2. Band der Literaturzeitung der Zeitschrift für Mathematik und
Physik 1857 erschienen ist.
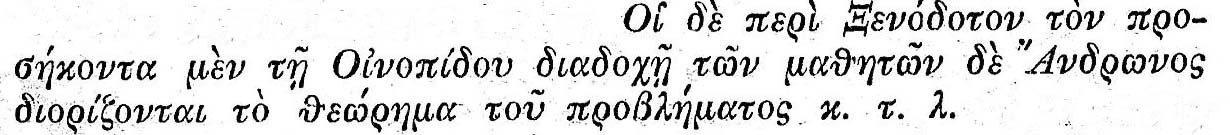
![]() Kontakt
Kontakt
![]() Historia Mathematica
Historia Mathematica
![]() Homo Heidelbergensis
Homo Heidelbergensis
![]() Heidelberger Texte zur Mathematikgeschichte
Heidelberger Texte zur Mathematikgeschichte