Felix Klein:
Geometer des Crelleschen Journals

Plücker

Mit Julius Plücker treten wir nun schon in die Periode ein, der wir selber durch viele Beziehungen verbunden sind. Ich selbst verehre in ihm meinen Lehrer, dessen physikalischer Assistent ich von 1866 bis 1868 gewesen bin, und dem ich auch durch Heimatsbeziehungen nahe stehe.

Plücker war eine viel weltläufigere Erscheinung als Moebius; er pflegte besonders lebhafte Beziehungen zu Frankreich und England, während sich das Verhältnis zu Berlin, wie schon angedeutet, unfreundlich gestaltete. Plücker bildet einen ungewöhnlichen Entwicklungstypus. Vom fünfunddreißigsten Lebensjahr ab vereinigte er die mathematische und physikalische Professur in Bonn und wurde durch diese Umstände allmählich seiner bisherigen mathematischen Arbeit entzogen, um sich ganz experimentalphysikalischen Forschungen hinzugeben. Erst gegen Ende seines Lebens kehrte er zur Geometrie zurück, ein Umstand, der für meine eigene Entwicklung (Herausgabe der Plückerschen Werke) entscheidend wurde.

Die Familie Plückers, der niederrheinischen Industrie angehörig, war in der Zeit der Religionswirren aus Aachen verbannt und nach Elberfeld übergesiedelt. Hier wurde Plücker am 16. August 1801 geboren. Er besuchte das Düsseldorfer Gymnasium, studierte in Bonn und Paris 1823/24 und habilitierte sich 1825 in Bonn, wo er 1828 außerordentlicher Professor wurde. 1832-34 war er außerordentlicher Professor in Berlin, zugleich am Friedrich-Wilhelm-Gymnasium tätig. Auch auf ihn fiel vorübergehend die Wahl zum zukünftigen Direktor des geplanten polytechnischen Instituts, das damals freilich schon als Oberlehrerbildungsanstalt gedacht war. Aus Plückers Berliner Zeit her schreibt sich wohl die Verschärfung des Konflikts mit dem Jacobi-Steinerschen Kreis. Steiner selbst kam 1835 als Extraordinarius an die Berliner Universität, als Plücker bereits seit einem Jahr Ordinarius in Halle war. 1836 wurde er nach Bonn berufen, wo durch von Münchows Tod drei Professuren: Mathematik, Physik und Astronomie verwaist waren. Die letztere fiel Argelander zu, die beiden anderen hatte Plücker bis zu seinem Tode (22. Mai 1868) inne.

Physik

Bei der Besprechung von Plückers Werken möchte ich zunächst auf seine physikalischen Leistungen eingehen wegen der persönlichen Beziehungen, die uns Göttinger damit verbinden. Plückers physikalische Abhandlungen sind zusammengefaßt im zweiten Band der von der Göttinger Gesellschaft der Wissenschaften gesammelten Abhandlungen, versehen mit einer Vorrede von Riecke.

Obwohl von der Mathematik ausgehend, war Plücker nichts weniger als ein mathematischer Physiker. Ihn reizte vielmehr die rein experimentelle Forschung, mit der er, dem Beispiel Faradays folgend, am liebsten in ganz unbekanntes Gebiet eindrang. So gelangen ihm eine ganze Reihe von Entdeckungen. 1847 bemerkte er die Erscheinung des Kristallmagnetismus an einer zwischen den Polen eines Elektromagneten aufgehängten Turmalinplatte, die sich, je nach ihrer Aufhängung axial oder transversal einstellt(1). Von 1857 an beobachtete er die Einwirkung des Magneten auf die elektrische Entladung in verdünnten Gasen, insbesondere auf die positive Entladung und das negative Glimmlicht; bei diesen Beobachtungen gelangte er bis dicht an die Erkenntnis der Kathodenstrahlen heran, die dann sein Schüler Hittorf vollendete. Auch das Ausziehen der Geißlerschen Röhren zu Kapillaren und die dadurch ermöglichten ersten Beobachtungen der Entladungsspektra wurden 1857 (Bd. 2, S. 502) von Plücker ausgeführt. Er erkannte die Spektra als Attribute der Gase und beobachtete insbesondere die drei ersten Wasserstofflinien. 1864 erreichte er mit Hittorf (Bd. 2, S. 665 ff.) viel genauere Ergebnisse und entdeckte insbesondere die durch die Natur der elektrischen Entladung bedingten Doppelspektra (Linien resp. Bandenspektra). Die abschließenden Arbeiten über diese Dinge finden sich sämtlich in den Philosophical Transactions. Aber auch diese Dinge fanden in Deutschland, gehemmt durch den Berliner Einfluß, keine Anerkennung. In Heidelberg begannen Kirchhoff und Bunsen 1858 mit der Spektralanalyse, beobachteten aber zunächst nur die einfachen Spektra der Metalldämpfe. Eine verschiedene Natur des Spektrums ein und desselben Gases bei verschiedenen Bedingungen des Leuchtens ist ihnen nicht entgegengetreten. Beiläufig gedenke ich der Ablehnung, welche Hittorf noch später, als er seine großartigen Entdeckungen betreffend die Kathodenstrahlen den Berliner Physikern Magnus, Poggendorff u. a. vorführte, in Berlin erfuhr. Die Gegensätze, welche wir hiermit berühren, reichen ziemlich bis zur Gegenwart heran.

Geometrie

Ich komme nun zur Fortführung unseres eigentlichen Gegenstandes, indem ich mich Plückers geometrischen Arbeiten zuwende. Fünf große selbständige Publikationen verdanken wir ihm außer den in Bd. 1 der gesammelten Abhandlungen abgedruckten Arbeiten:
  1. Analytisch-geometrische Entwicklungen, Bd. 1 u. 2. 1828, 1831.
  2. System der analytischen Geometrie (der Ebene). 1834.
  3. Theorie der algebraischen Kurven. 1839.
  4. System der analytischen Geometrie des Raumes. 1846.
  5. Neue Geometrie des Raumes, gegründet auf die Betrachtung der geraden Linie als Raumelement. 1868, 1869 (Teil II posthum von mir herausgegeben).
Über das letzte Werk, das Plückers zweiter geometrischer Periode entstammt, werde ich erst im späteren Verlauf dieser Vorträge sprechen. Als einen bemerkenswerten Zug aber möchte ich anführen, daß der Wiederbeginn von Plückers geometrischen Arbeiten mit Steiners Todesjahr 1863 zusammenfällt. Ob hier ein Zusammenhang vorliegt, kann natürlich nicht entschieden werden.

Plückers Ziel in der Geometrie und seine Leistung ist der Neuaufbau der analytischen Geometrie. Er verfolgte dabei eine aus der Mongeschen Tradition weitergebildete Methode: das völlige Zusammenwachsen von Konstruktion und analytischer Formel. In der Vorrede seines ersten Werkes, S. IX, sagt er: „Ich möchte mich zu der Ansicht bekennen, daß die Analysis eine Wissenschaft ist, die, unabhängig von jeder Anwendung, selbständig für sich allein dasteht, und die Geometrie, so wie von einer anderen Seite die Mechanik, bloß als bildliche Deutung gewisser Beziehungen aus dem großen, erhabenen Ganzen erscheint.“ In diesen Worten klingen deutlich Auffassungen von Monge nach, die wir in anderer Form bei Gauß kennen lernten.

In der Plückerschen Geometrie wird die bloße Kombination von Gleichungen in geometrische Auffassung übersetzt und rückwärts durch letztere die analytische Operation geleitet. Rechnung wird nach Möglichkeit vermieden, dabei aber eine bis zur Virtuosität gesteigerte Beweglichkeit der inneren Anschauung, der geometrischen Ausdeutung vorliegender analytischer Gleichungen ausgebildet und in reichem Maße verwendet.

Zum Pascalschen Satz

Als Beispiel für die Plückersche Denkweise gebe ich seinen Beweis des Pascalschen Satzes.

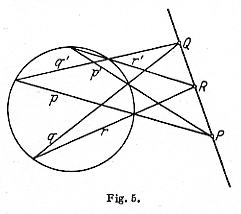Es handelt sich um zwei Tripel von Geraden p, q, r und p', q', r', von deren neun Schnittpunkten sechs auf einem Kegelschnitt liegen (vgl. Fig. 5). Es wird behauptet, daß die übrigen drei auf einer geraden Linie liegen. Wir betrachten p, q, r, p', q', r' als lineare Ausdrücke, deren Nullsetzung die Gleichungen der sechs in Frage kommenden Geraden ergeben. Dann ist die Kombination pqr - μp'q'r' = 0 die Gleichung eines Büschels von Kurven dritter Ordnung, die sämtlich durch die neun Schnittpunkte der beiden Geradentripel gehen. Da nun von den neun Punkten sechs auf dem Kegelschnitt liegen und in dem μ noch eine Konstante zu freier Verfügung steht, so kann ich durch geeignete Wahl von μ eine Kurve herausgreifen, die noch einen siebenten Punkt mit dem Kegelschnitt gemein hat. Eine C3 und eine C2 haben aber im allgemeinen nur sechs Schnittpunkte. Besitzt die Gleichung sechsten Grades, die ihren Schnitt bedingt, mehr als sechs Wurzeln, so ist sie identisch Null. Folglich muß die C3 zerfallen in den Kegelschnitt selbst und einen linearen Restbestandteil, der notwendig die drei anderen Schnittpunkte der beiden Geradentripel enthalten muß. Also liegen diese drei Punkte auf einer Geraden.

Dieser Beweis, der bei einiger Übung so einleuchtet, daß er sogar noch kürzer gefaßt werden könnte, zeigt gleich noch zwei andere Plückersche, sehr wertvolle Eigenheiten. Das eine ist die „abgekürzte Bezeichnungsweise“, die sich mit der Benennung einer Gleichung begnügt, ohne sie explizite hinzuschreiben; das zweite ist der von Plücker bei jeder Gelegenheit verwendete unbestimmte Koeffizient, „das Plückersche μ“. Dies μ findet sich hie und da auch schon in Gergonnes Annalen. (Auch Steiner war es bekannt, aber nur von Jacobis Seite, weshalb er das μ als „,Judenkoeffizienten“ bezeichnete.) Aber erst bei Plücker wurde es zu einem wesentlichen Werkzeug, das ihm große Hilfe leistete in seiner Kunst, „,in den Gleichungen zu lesen“.

Dreieckskoordinaten, beliebiges Raumelement

Zu der charakterisierten, allgemeinen Methode Plückers treten nun die Fortschritte im einzelnen. Von der Einführung der allgemeinsten homogenen Dreieckskoordinaten und ihrem Vorzug wurde bereits gesprochen — sie werden im „System“ 1834 definiert als die mit willkürlichen Konstanten multiplizierten Abstände des Punktes P von den Dreiecksseiten; in Crelle, Bd. 5, 1830, sind noch die Abstände selbst als Koordinaten eingeführt, wodurch eine ähnliche Beschränkung resultiert wie bei Moebius. Durch diese Einführung werden nun sämtliche Gleichungen der geometrischen Gebilde homogen, was infolge des Eulerschen Theorems über homogene Funktionen sehr elegante Darstellungen ermöglicht, die von Plücker in der weitestgehenden Weise ausgebildet werden. Insbesondere die Tangenten- und Polarenlehre erfährt eine völlige Umbildung, Wenn f = 0 einen Kegelschnitt bedeutet, der den Punkt x, y, z enthält, so stellt nämlich die Gleichung
δ f
δ x		 · x' + δ f
δ y 		· y' + δ f
δ z 		· z' = 0
je nach Auffassung der x', y', z' oder der x, y, z als laufende Koordinaten, entweder die Tangente der Kurve f = 0 in dem festen Punkte x, y, z dar, oder die Polare des festen Punktes x', y', z' in Bezug auf die Kurve f = 0. Der Wechsel dieser Auffassung wird bis zur Virtuosität ausgebildet und zu eleganten Beweisen aller Arten von Theoremen verwendet.

Durch die homogenen Koordinaten gelingt nun auch eine glänzende analytische Realisierung der kühnen Ponceletschen Konzeptionen der unendlich fernen Geraden, der Kreispunkte usw. Die Kreisgleichung (x - a)2 + (y - b)2 = r2 geht durch Einführung von

x = x1
x3		,  y = x2
x3		   über in   (x1 - ax3}2 + (x2 - bx3)2 = r2 x32.
Die Gleichung der unendlich fernen Geraden x3 = 0 ergibt nun in der Tat für jeden beliebigen Kreis das Durchschnittsgebilde x12 + x22 = 0, d. h. das Punktepaar, das durch die Koordinaten x1 : x2 : x3 = 1 : +i : 0 und x1 : x2 : x3 = 1 : -i : 0 gegeben ist; das sind aber gerade die sog. Kreispunkte.

Nicht minder wichtig als die Einführung der homogenen Koordinaten ist folgende neue Gedankenwendung. Die Gleichung der Geraden u1x1 + u2x2 + u3x3 = 0 ist in den Koeffizienten u und den Koordinaten x völlig symmetrisch. Plücker faßt nun die u als veränderliche Größen auf, deren jedes System eine Gerade durch den festgehaltenen Punkt x1 , x2, x3 bezeichnet. Er nennt die u1, u2, u3 „Linienkoordinaten“; in ihnen drückt die obenstehende Gleichung das durch den Punkt gehende Strahlbüschel, d. h. diesen Punkt selber aus. So gut wie ich die lineare Relation als Gleichung einer Geraden in Punktkoordinaten auffassen kann, so berechtigt bin ich auch, die Gleichung eines Punktes in Linienkoordinaten in ihr zu sehen.

Mit diesem Gedanken des beliebigen „Raumelements“, das zum Ausgangspunkt der Geometrie gewählt werden kann, ist nun eine völlige Klärung des Poncelet-Gergonneschen Prinzips der Dualität gegeben: Weil die Gleichung für die vereinigte Lage von Punkt und Gerade (im Raume von Punkt und Ebene) in den zweierlei Elementen symmetrisch ist, kann man in allen Sätzen, die auf bloße Verknüpfung der beiden Elemente begründet sind, die beiden Worte vertauschen!

Dies sind die wesentlich neuen Gedanken, die Plücker in das vielbebaute Gebiet der Geometrie der linearen und quadratischen Gebilde hineintrug. Darüber hinaus ergreift er nun ganz neue Objekte der Untersuchung. Während die französischen Geometer sich auf das angegebene Gebiet meist beschränkt hatten, Poncelet bei den ersten weitergehenden Versuchen auf Schwierigkeiten geraten war, gelingt nun Plücker der erste erfolgreiche Vorstoß auf die allgemeine Theorie der algebraischen Kurven der Ebene.

Plückersche Formeln

Als Hauptleistung möchte ich hier die „Plückerschen Formeln“ nennen, welche die Ordnung einer Kurve n (Grad der Gleichung in Punktkoordinaten) mit der Klasse k (Grad der Gleichung in Linienkoordinaten) und den einfachen (sog. notwendigen) Singularitäten verknüpfen(2). Sie finden sich am Schluß des „Systems“ von 1834. Zunächst fand Plücker die Beziehung k = n(n-1) - 2d - 3r, wo d die Anzahl der Doppelpunkte, r die der Rückkehrpunkte der Kurve bezeichnet. Diese Gleichung ließ sich nicht ohne weiteres, etwa durch Vertauschung von n und k dualisieren. Dem Prinzip der Dualität wurde erst Genüge getan durch die Entdeckung und Einführung der sog. „Liniensingularitäten“. Den Doppelpunkten d entsprechen dualistisch die Doppeltangenten t, den Rückkehrpunkten r die oskulierenden; d. h. die Kurve durchdringenden Wendetangenten w, deren Berührungspunkte man als Wendepunkte bezeichnet. Für die Anzahl dieser Wendepunkte fand Plücker die Beziehung w = 3 n (n - 2), die sich im Falle des Auftretens von Punktsingularitäten in
w = 3n (n- 2) - 6d - 8r
verwandelt. Damit ist nun das Material gewonnen, aus dem durch Dualisieren das volle Formelnsystem der Singularitäten hervorgeht:
k= n(n - 1) - 2d - 3r,   n= k (k - 1) - 2t - 3w,
w=3n(n - 2)-6d-8r,   r = 3 k (k- 2) - 6t - 8w.

Im Falle n = 3, d = 0, r = 0 ergibt sich w = 9. Bis dahin waren nur drei Wendepunkte der allgemeinen Kurve dritter Ordnung C3 bekannt gewesen, und Plücker beweist, daß sechs von den neun immer imaginär sein müssen. Es war nun schon im 18. Jahrhundert von Maclaurin bewiesen, daß die drei reellen Wendepunkte der C3 auf einer Geraden, der „Wendelinie“, liegen. Da die reellen Wendepunkte keine ausgezeichnete Eigenschaft vor den übrigen besitzen im Sinne der allgemeinen Lagengeometrie, muß dieser Satz auch für jedes andere Tripel von Wendepunkten gelten. Der Beweis läßt sich, ganz ähnlich wie oben der des Pascalschen Satzes, durch abgekürzte Bezeichnung führen. Die C3 besitzt folglich zwölf Wendelinien, deren einfachstes Schema später von Hesse gegeben wurde. Dies Beispiel möge zeigen, welche Bereicherung die Geometrie der Kurven durch Plückers Entdeckung erfuhr. S. VI des „Systems“ von 1834 äußert er sich selbst: „Es ist ein neuer Flug der Anschauung nötig, um das zu ergreifen, was in allen Fällen imaginär ist und imaginär bleibt.“

Daß die Trainierung der Anschauung nötig sei, um in dieser neuen Geometrie sicher zu gehen, zeigt Plückers Beispiel selbst, der sich bei der Anordnung der 28 Doppeltangenten der allgemeinen C4 in Irrtümer verstrickte (Algebraische Kurven, 1839). Aus der Zahl der willkürlichen Konstanten der allgemeinen C4 schließt er — auch eine spezifische Plückersche Schlußweise — mit Recht, daß ihre Gleichung sich in die Form Ω2 - μpqr s = 0 setzen läßt, wo Ω = 0 einen Kegelschnitt, p =0, q = 0, r=0, s = 0 Geraden bedeuten, die dann Doppertangenten der C4 sind. Aber irrtümlicherweise leitet er hieraus den Satz ab, daß die Berührungspunkte von je vier Doppeltangenten auf einem Kegelschnitt lägen, während die Behauptung nur für eine bestimmte Auswahl und Zusammenstellung von vier Tangenten richtig ist. Die p, q, r, s sind nämlich nicht alle vier frei wählbar, sondern nach Auswahl von zweien sind die beiden anderen auf fünffache Weise bestimmt. (Dieser Fehler wurde später von Steiner nachgewiesen.)

Nach einer Seite freilich lassen die Plückerschen Formeln trotz ihrer großen Leistungsfähigkeit noch Probleme offen; sie liefern nichts zur Trennung des Reellen und Imaginären. Wenn auch dem abstrakten Denken diese Fragen jahrzehntelang gleichgültig waren, so haben sie doch das größte Interesse für den, der die wahre geometrische Gestalt des Gebildes zu erforschen sucht, und es ist entschieden als ein Auswuchs der modernen Geometrie zu betrachten, wenn das Gewicht dieser Frage überhaupt geleugnet wird. Diese Probleme des Verhaltens geometrischer Gebilde nach Seite ihrer Realität liegen im allgemeinen sehr tief und fordern weit in die algebraische Natur der Gleichung eindringende Forschungen. Um so lieber nenne ich hier eine 1876 von mir gefundene Formel (Math. Ann. Bd. 10 = ges. Abh. Bd. 2, S. 78ff.), die allein mit den Plücker zu Gebote stehenden Mitteln auf elementarem Wege abzuleiten ist, und seine Formeln nach dieser Seite wenigstens zu einem gewissen Teil ergänzt. Bezeichnet w' die Zahl der reellen Wendepunkte, t" die der reellen isolierten Doppeltangenten, r' und d" entsprechend die der reellen Rückkehrpunkte und reellen isolierten Doppelpunkte, so ist

n + w' + 2t" = k + r' + 2d".
Durch diese Formel ist z. B. die Frage nach der Realität der Wendepunkte der C3 erledigt. Aus
3 + w' + 0 = 6 + 0 + 0
ergibt sich w' = 3. Der Satz von der Realität der Wendepunkte der C3 tritt also aus seiner isolierten Stellung heraus.

Daß Plücker diese Formel, die auf seinem Wege lag, nicht gekannt hat, ist um so bedauerlicher, als sie bei seinem großen Interesse an der wahren geometrischen Gestalt der Kurven ihm gewiß willkommen gewesen wäre. Plücker war bei all seinen Leistungen zum Ausbau der projektiven Geometrie kein Projektiviker im eigentlichen Sinne. Im Stile der alten Geometer des 18. Jahrhunderts haftete er am Konkreten, richtete sein Augenmerk auf das Verhalten der Kurve im Unendlichen, widmete z. B. ausführliche Untersuchungen der Frage nach den Asymptoten usw., alles Dinge, deren Bedeutung vom rein projektiven Standpunkt aus verschwindet. Die konsequente Durchbildung des projektiven Denkens und damit die Ausgestaltung der Invariantentheorie blieb einer späteren Generation vorbehalten.

Anmerkungen:

  1. Diese Untersuchungen sind zu einem gewissen Abschluß gebracht in dem Buche von A. Beer: Einleitung in die Elektrostatik, die Lehre vom Magnetismus und die Elektrodynamik, Braunschweig 1865, herausgegeben von Plücker.
  2. Poncelet hatte sich nicht erklären können, warum man nicht die Beziehung k = n (n- 1) in n = k (k - 1) dualisieren durfte („Ponceletsches Paradoxon“).

S. 119-126 aus
Klein, Felix: Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. - Teil 1. - Berlin : Springer, 1926. - XIII, 385 S.
Signatur UB Heidelberg: L 234:: 24,1.1926

Letzte Änderung: 24.05.2014     Gabriele Dörflinger   Kontakt

Zur Inhaltsübersicht     Historia Mathematica     Homo Heidelbergensis     Heidelberger Texte zur Mathematikgeschichte