Felix Klein:
Vertiefte Einsicht in das Wesen algebraischer Gebilde.

Hilbert

Hilbert, geb. 1862 in Königsberg, hat dort, mit kurzen Unterbrechungen, die wesentlichen Stufen seiner Entwicklung durchlaufen: Student, Dozent, Extraordinarius, bis er 1895 als Ordinarius nach Göttingen kam. - - - - - Hilberts rastloser Geist hat im Laufe der Jahre wechselnd sich auf den verschiedensten Gebieten der Mathematik betätigt. Die Arbeiten, die uns gegenwärtig interessieren, und die man die Gedichte erster Periode nennen könnte, gehen von 1883 bis etwa 1898. Hilbert hat, seitdem er in Göttingen wirkt, immer zahlreiche Schüler angezogen (in Königsberg war dazu noch wenig Gelegenheit, zumal in den damaligen Jahren die mathematische Frequenz unserer Universitäten auf ein Minimum herabgesunken war). Aber die Schüler beherrschen immer nur das eine Gebiet, das sie gerade bei Hilbert gelernt haben, und kennen wohl meist nicht die Zusammenhänge, die uns hier in erster Linie interessieren.

Theorie der algebraischen Formen

Wir werden hier zwei Arbeiten von Hilbert charakterisieren. Zunächst die Arbeit über die Theorie der algebraischen Formen, Math. Ann., Bd. 36 (1890), wo Kroneckersche Ansätze mit Dedekindscher Denkweise zum Abschluß gebracht und davon eine glänzende Anwendung auf die Probleme der Invariantentheorie gemacht wird.

Wir erwähnen vor allen Dingen den Satz, daß jedes algebraische Gebilde beliebiger Ausdehnung in einem Raume von beliebig vielen homogenen Variablen x₁, … , x_n immer so durch eine endliche Anzahl homogener Gleichungen

F₁=0, F₂=0, … , F_μ = 0 dargestellt werden kann, daß die Gleichung F = 0 jedes anderen durch das Gebilde hindurchgehenden Gebildes in der Gestalt angeschrieben werden kann: M₁F₁+ … +M_μF_μ = 0, wo die M beliebige homogene (rationale, ganze) Formen sind, deren Grade nur so gewählt werden müssen, daß die linke Seite der Gleichung selbst wieder homogen ist.

Nach der in der Zahlentheorie von Gauß herrührenden Ausdrucksweise wird man sagen: Jede Form F, die unser Gebilde enthält, ist modulis F₁, F₂, … , F_μ kongruent Null. — Im übrigen schließt sich Hilbert der Dedekindschen Denkweise so weitgehend an, daß er die Gesamtheit unserer Formen selbst einen Modul nennt! Der Hilbertsche Satz heißt dann: Jedes algebraische Gebilde des R_n bedingt das Verschwinden eines „endlichen Moduls“(1).

Beispiel: Raumkurve dritter Ordnung

Als Beispiel wähle ich die Raumkurve dritter Ordnung. Diese wird durch den partiellen Schnitt zweier F₂ erhalten. Man sieht das folgendermaßen ein: Wir denken uns die gegebene C₃ wieder auf einem einschaligen Hyperboloid liegen (vgl. oben S. 317 und Fig. 28, S. 319) und projizieren sie auf die Ebene. Die entsprechende ebene Kurve dritter Ordnung möge im Punkte O₂ einen Doppelpunkt haben (vgl. Fig. 32). Ziehen wir nun durch den anderen Fundamentalpunkt O₁ eine Gerade, so können wir diese Gerade und die C₃ zusammen als C₄ erster Spezies auffassen. 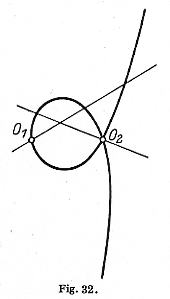Dieser C₄ entspricht im Raume der volle Schnitt einer F₂ mit dem Hyperboloid. Eine F₂, die das Hyperboloid in einer C₃ schneidet, hat also mit diesem außerdem noch eine Erzeugende gemein. Durch beide geht natürlich ein ganzes Büschel von Flächen zweiten Grades, nämlich λF₂ + μH = 0 (unter H = 0 die Gleichung des Hyperboloids verstanden). Entsprechend dem Geradenbüschel durch O₁ gibt es eine einfach-unendliche Schar von Büscheln λF₂ + μH = 0, die das Hyperboloid in der C₃ und je in einer Erzeugenden schneiden, womit ich ∞² Flächen zweiten Grades erhalte λF₂ + λ' F₂' + μH = 0, die durch die C₃ gehen. Es fragt sich nun, wieviele Flächen F₁, … , F_μ muß man durch die C₃ legen, damit jede andere durch die C₃ gehende Fläche F in der gewünschten Gestalt

F = M₁F₁ + M₂F₂ + … + M_μF_μ = 0 erscheint? Es zeigt sich, daß dazu die drei Flächen zweiten Grades F₂, F₂' und H genügen.

Den zugehörigen dreigliedrigen Modul erhalten wir am einfachsten, indem wir die drei Unterdeterminanten einer Matrix von 2·3 linearen Formen gleich Null setzen. Diese Matrix sei

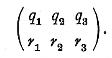
Dann sind F_κ = q_λr_μ - r_λq_μ = 0 (κ, λ, μ = 1, 2, 3) Flächen zweiten Grades, die nur eine C₃ gemein haben, und die zugleich den zugehörigen Modul definieren.

Der Beweis des Hilbertschen Satzes und anderer Sätze ist sehr abstrakt, aber an sich ganz einfach und darum logisch zwingend. Eben darum leitet diese Arbeit von Hilbert eine neue Epoche der algebraischen Geometrie ein.

Ebenso einfach ist dann auch die Anwendung auf die Invariantentheorie, die ich hier noch weniger zergliedern kann. Die ganze Frage der Endlichkeit der Invarianten, welche Gordan seinerzeit nur mit umfangreichen Rechnungen für binäre Formen hatte erledigen können (vgl. oben S. 308), wird hier mit einem Schlage für Formen mit beliebig vielen Veränderlichen gelöst.

Ihrer Eigenart entsprechend wurde diese Arbeit zunächst mit sehr verschiedener Stimmung aufgenommen. Mich hat sie damals bestimmt, Hilbert bei nächster Gelegenheit nach Göttingen zu ziehen. Gordan war anfangs ablehnend: „Das ist nicht Mathematik, das ist Theologie.“ Später sagte er dann wohl: „Ich habe mich überzeugt, daß auch die Theologie ihre Vorzüge hat.“ In der Tat hat er den Beweis des Hilbertschen Grundtheorems selbst später sehr vereinfacht (Münchener Naturforscherversammlung 1899).

Hilberts Zahlbericht

An zweiter Stelle nennen wir den schon (S. 324) angeführten Zahlbericht von 1897, der sich äußerlich als ein Referat über die vorhandene Literatur gibt, aber nicht nur diese überall auf einfachere Grundlagen zurückführt, sondern weitgehend in neue Fragestellungen vorstößt.

Ich möchte von dem inneren Gedanken, der Hilbert dabei geleitet hat, nämlich der Analogie der Zahlkörper mit den Funktionenkörpern, einen Begriff geben, und zwar um so lieber, als sich Hilbert selbst hierüber erst später und nur beiläufig ausgesprochen hat, nämlich in seinem Vortrag über „Mathematische Probleme“ auf dem Pariser Internationalen Mathematiker-Kongreß, 1900 (Bericht S. 58 ff.; Göttinger Nachrichten 1900; siehe Nr. 12 daselbst).

Exkurs über Galoissche Theorie

Aber um hier verständlich zu reden, muß ich (unter Berufung auf Kap. 2, S. 89 ff.) eine Einschaltung machen über die Galoissche Theorie der algebraischen Gleichungen. Ich resümiere die Hauptpunkte.

Die Grundlage der Galoisschen Theorie ist, wie ich damals schon ausführte, der Begriff des Rationalitätsbereiches. — Als rational können angesehen werden: zunächst entweder nur die Zahlen m/n, wo m und n gewöhnliche ganze Zahlen sind, oder alle rationalen Funktionen irgendwelcher Parameter r(z₁, z₂, … , z_n) mit rationalen oder auch beliebigen Koeffizienten. Ferner kann man den Rationalitätsbereich noch erweitern, indem man irgendwelche feste algebraische Irrationalitäten, z. B. bestimmte Einheitswurzeln, adjungiert und alle Funktionen, die aus solchen Irrationalitäten rational aufgebaut sind, zum Bereiche zählt. Endlich kann man noch den Rationalitätsbereich relativ zu einer über der z-Ebene ausgebreiteten Riemannschen Fläche definieren.

Der zweite Grundbegriff ist der der Irreduzibilität einer Gleichung. Es sei eine Gleichung

f(x) = 0 vorgelegt, deren Koeffizienten rationale Zahlen oder rationale Funktionen irgendwelcher Parameter oder auch adjungierter Irrationalitäten sein mögen. Die Gleichung ist „reduzibel“, wenn sie sich im vorgegebenen Rationalitätsbereiche in Faktoren spalten läßt. Z. B. ist die Gleichung x² + 5 = 0 „irreduzibel“ im gewöhnlichen Rationalitätsbereiche der Zahlen m/n. Adjungieren wir √ -5, so wird sie reduzibel: x² + 5 = (x + √-5) (x - √-5). Die „Irreduzibilität“ einer Gleichung ist also ein relativer Begriff, sie ist immer bezogen auf den vorher definierten Rationalitätsbereich.

Die Gleichung f(x) = 0 sei nun im gegebenen Rationalitätsbereiche irreduzibel. Ihre Wurzeln seien x₁, … , x_n.

Dann gibt es eine Gruppe von Vertauschungen der x₁, … , x_n, welche die Galoissche Gruppe genannt wird und die folgenden zwei Eigenschaften hat:

Jede Funktion R (x₁, … , x_n), welche bei den Vertauschungen der Gruppe numerisch ungeändert bleibt, ist rational bekannt.
Umgekehrt bleibt jede rationale Funktion R (x₁t … , x_n), die einen rationalen Wert hat, bei den Vertauschungen der Gruppe numerisch ungeändert.

Von der Struktur dieser Gruppe (ihren Untergruppen usw.) hängt es ab, was man über die Auflösbarkeit der Gleichung, über die Art ihrer Resolventen usw. sagen kann. —

Das Wesentliche für uns ist hier, daß die Galoissche Theorie sowohl für numerische Gleichungen f (x) = 0, die einen Parameter enthalten, als auch für Funktionenkörper gilt.

Betrachten wir zunächst den letzteren Fall. Rational soll also heißen, was eine rationale Funktion von z ist, wobei wir von der numerischen Natur der in diesen rationalen Funktionen vorkommenden Koeffizienten ganz absehen wollen. In diesem Falle haben wir eine anschauliche Art, den Begriffen „Irreduzibilität“ und „Gruppe“ nahezukommen :

Wir konstruieren uns zunächst über der z-Ebene die zu ζ gehörige Riemannsche Fläche. Wenn diese Fläche aus einem Stücke besteht, so ist die Gleichung irreduzibel und umgekehrt!

Wir wollen uns jetzt die Verzweigungsstellen a, b, … , k der Gleichung f (ζ, z) = 0 in der z-Ebene markieren und durch eine beliebige Kurve ohne Doppelpunkte verbinden. Schneiden wir nun längs dieser Kurve alle Blätter der Riemannschen Fläche zugleich durch, so zerfällt diese in n getrennte Blätter, die wir mit ζ₁, … , ζ_n bezeichnen wollen. Über den Verzweigungspunkten können natürlich gewisse Blätter der Riemannschen Fläche schlicht verlaufen. Wir schreiben uns für jedes Stück des Schnittes zwischen zwei Verzweigungspunkten auf, wie dort die Blätter an einander geheftet sind, d. h. wir stellen eine Tabelle des Blätterzusammenhanges auf. So oft wir unseren Schnitt überschreiten, so findet eine Vertauschung der Blätter statt, die wir aus unserer Tabelle ablesen können.

Indem wir z alle möglichen geschlossenen Wege durchlaufen lassen, erhalten wir eine Gruppe von Vertauschungen, die wir sonst die Monodromiegruppe der Gleichung nannten. (Diesen Ausdruck gebrauchten wir schon in dem allgemeinen Falle der linearen Differentialgleichungen vgl. S. 268.) Diese Monodromiegruppe ist bei Zugrundelegung des von uns verabredeten Rationalitatsbereiches die Galoissche Gruppe der vorgelegten Gleichung. Denn es ist klar

daß jede Funktion R (ζ, z), die dabei ungeändert bleibt, eben deshalb, eine rationale Funktion von z allein ist (eine algebraische Funktion von z, die eindeutig ist, ist rational),
daß jede rationale Funktion r (z), weil sie eindeutig ist, bei den Umläufen der z gewiß ungeändert bleibt.

Wir sehen, wie unsere Riemannsche Fläche, wenn eben wir den Parameter z der Definition des Rationalitätsbereichs zugrunde legen, mit den Galoisschen Ideen zusammenhängt, und wie diese wiederum mit Hilfe der Riemannschen Fläche veranschaulicht werden können: Statt die Riemannsche Fläche zu geben, kann ich die Verzweigungsstellen a,b,…,k vorschreiben und angeben, welche Vertauschungsgruppen durch deren Umlaufung zustande kommen. Damit gehen wir sozusagen von Riemann zurück zu Puiseux, der schon 1851 solche Gruppen aufgestellt hat(2).

Übertragung auf die Zahlkörper

Hierin aber liegt die wunderbare Möglichkeit, nicht die Riemannsche Fläche selbst, aber die aus ihrer Betrachtung folgenden Theoreme oder wenigstens die Fragestellungen auf Zahlkörper zu übertragen. Denn an Stelle der Verzweigungsstellen a, b, …, k treten, wie wir bereits wissen, die Primfaktoren des „wesentlichen“ Teilers der Diskriminante, und der Galoisschen Gruppe im algebraischen Funktionenkörper entspricht natürlich die Galoissche Gruppe im Zahlkörper.

Dieses Entsprechen wird nun dadurch für die Zahlentheorie sehr fruchtbar, daß man für die Riemannsche Fläche Sätze kennt, die über unsere algebraischen Hilfsmittel hinausliegen, und deren Analogie für den Zahlkörper man nun suchen kann.

Da ist vor allen Dingen der Riemannsche Existenzsatz, den wir hier so aussprechen: Zu jeder über der z-Ebene vorgegebenen algebraischen Riemannschen Fläche gehört ein Körper R (ζ, z).

Ferner kann man fragen: Was entspricht im Zahlkörper den einfachen Formulierungen, die durch Betrachtung der Abelschen Integrale gewonnen werden, dem Abelschen Theorem usw. ?

Hiermit haben wir nun den eigentlichen Schlüssel zu den Neuentwicklungen in Hilberts Zahlbericht und seinen zugehörigen späteren Arbeiten resp. denjenigen seiner Freunde und Schüler. Hilbert wollte, die zahlentheoretischen Entwicklungen möglichst dahin bringen, daß der Zahlkörper durch seine Diskriminante und die zugehörige Galoissche Gruppe definiert erscheint und sämtliche in der Funktionentheorie bekannten Sätze sich wiederfinden! (vgl. das zwölfte der Probleme von 1900). Er hat dieses Ziel allerdings nur in einigen Fällen voll erreicht. Insbesondere beim sog. „Klassenkörper'', der zu einem Rationalitätsbereich K(√ -D) gehört. Die Galoissche Gruppe ist hier eine Abelsche Gruppe, d. h. sie besteht aus lauter vertauschbaren Operationen, und die Diskriminante (relativ zu dem Körper K(√-D) ist 1. Die vollen Beweise hat erst Furtwängler gegeben. Es ist unmöglich, daß ich hier mehr ins Einzelne gehe. Aber es ist doch, denke ich, einiges gewonnen, wenn wir solcherweise den leitenden Grundgedanken kennen.

Schluß, Ausblick auf weitere Aufgaben

Nun ist es Zeit, unser Kap. 7 zu schließen. Ich beschränke mich darauf, noch einmal das allgemeinste Problem, welches hier vorliegt, im Anschluß an Kroneckers Festschrift von 1881 (Crelle, Bd. 92) zu charakterisieren. Es handelt sich nicht nur um die reinen Zahlkörper oder Körper, die von einem Parameter z abhängen, oder um die Analogisierung dieser Körper, sondern es handelt sich schließlich darum, für Gebilde, die gleichzeitig arithmetisch und funktionentheoretisch sind, also von gegebenen algebraischen Zahlen und gegebenen algebraischen Funktionen irgendwelcher Parameter algebraisch abhängen, das selbe zu leisten, was mehr oder weniger vollständig in den einfachsten Fällen gelungen ist.

Es bietet sich da ein ungeheurer Ausblick auf ein rein theoretisches Gebiet, welches durch seine allgemeinen Gesetzmäßigkeiten den größten ästhetischen Reiz ausübt, aber, wie wir nicht unterlassen dürfen hier zu bemerken, allen praktischen Anwendungen zunächst ganz fern liegt. Damit ist natürlich nicht gesagt, daß das immer so zu bleiben braucht.

Anmerkungen.

In neuerer Zeit nennt man in Anlehnung an Dedekind die im Texte besprochene Gesamtheit ein Ideal und wendet die Bezeichnung „Modul“ für allgemeinere Gesamtheiten an. Anm. d. Herausg. [Richard Courant und Otto Neugebauer]
Vgl. Enzyklop. I B 3c, d S. 487.

S. 328-334 aus
Klein, Felix: Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. - Teil 1. - Berlin : Springer, 1926. - XIII, 385 S.
Signatur UB Heidelberg: L 234:: 24,1.1926

Letzte Änderung: 24.05.2014 Gabriele Dörflinger Kontakt

Zur Inhaltsübersicht Historia Mathematica Homo Heidelbergensis Heidelberger Texte zur Mathematikgeschichte

Felix Klein: Vertiefte Einsicht in das Wesen algebraischer Gebilde.