Sof'ja Kowalewskaja: Promotion in Göttingen

Berlin, 27. Juni 1874.

Zunächst habe ich Ihnen meinen verbindlichsten Dank für die Bereitwilligkeit auszusprechen, mit der Sie sich sofort nach Ihrer Ankunft in Göttingen der Mühe unterzogen haben, mir inbetreff der Promotionsangelegenheit meiner Schülerin, der Frau VON KOWALEWSKY, die gewünschte Auskunft zu verschaffen. Was Sie in Ihrem Briefe vom 18. April d. J. mir mitteilen, ist mir unmittelbar darauf von Herrn Prof. Weber, den hier in Berlin einmal wieder sprechen zu können mir eine große Freude gewesen ist, vollständig bestätigt worden, wobei ich von demselben noch die interessante Notiz erhielt, daß Gauß, als es sich bei Gelegenheit der letzten Jubelfeier der Göttinger Universität um die zu vollziehenden Ehrenpromotionen handelte, nichts mehr bedauert habe, als daß Sophie Germain nicht mehr am Leben sei, welche der Welt bewiesen habe, daß auch eine Frau in der strengsten und abstraktesten der Wissenschaften etwas Tüchtiges zu leisten imstande sei und darum ein Ehrendiplom wohl verdient haben würde.

Hiernach habe ich kein Bedenken getragen, Frau von Kowalewsky zu ermutigen, sich bei Ihrer Fakultät um die Promotion in absentia zu bewerben und zu dem Zweck einige Arbeiten, mit denen sie sich im letzten Jahre teils aus eigenem Antrieb, teils auf meine Veranlassung beschäftigt hat, fertig zu machen. Auf meinen Rat wird sie der Fakultät drei Abhandlungen vorlegen, um den Beweis zu liefern, daß sie auf verschiedenen Gebieten der Mathematik heimisch genug geworden ist, um im Anschluß an Vorhandenes selbständige und für die Wissenschaft ersprießliche Untersuchungen anzustellen. Eine dieser Abhandlungen beschäftigt sich mit der Frage, ob und wie weit sich die Sätze über die Integration eines Systems gewöhnlicher Differentialgleichungen durch Potenzreihen, welche ich zuerst in meiner Abhandlung über die analytischen Fakultäten (Crelles Journal 51, S, 43,44) aufgestellt habe und die bald darauf von den Herren Briot und Bouquet bewiesen worden sind, auf den Fall ausdehnen lassen, wo zur Bestimmung von Funktionen mehrerer Veränderlichen die erforderliche Anzahl von partiellen Differentialgleichungen gegeben ist. Die Frage mußte unbedingt einmal gründlich erörtert werden; ich selbst habe, offen gestanden, Scheu gehabt, mich darauf einzulassen, und es freut mich umso mehr, daß sie in der in Rede stehenden Arbeit, die in ihrer letzten Redaktion nur von mäßigem Umfange ist, auf die gründlichste Weise erledigt worden ist. Schwierigkeiten, die sich zunächst darboten, z. B. die unerwartete und Bedenken erregende Bemerkung, daß schon eine so einfache Differentialgleichung, wie die so oft behandelte

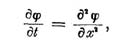
In der zweiten Abhandlung sind die LAPLACEschen Untersuchungen über die Gestalt der Saturnsringe wieder aufgenommen und weitergeführt worden. Die Resultate von Laplace sind nur als erste Annäherung betrachtet gültig; ein Ring, der den Bedingungen des Problems, wie es von Laplace gestellt ist, genügen soll, kann nicht durch Umdrehung einer Ellipse um eine ihrer kleinen Axe parallele Gerade entstanden sein; an die Stelle der Ellipse muß vielmehr eine Figur treten, welche an ihren beiden Scheiteln verschieden gekrümmt ist und sich auch unter der von Laplace gemachten Annahme, wenn man von der Komplikation der Rechnung absieht, bis zu jedem Grade der Annäherung bestimmen läßt. Für die zweite Annäherung ist die Rechnung vollständig ausgeführt.

In einer dritten Abhandlung hat meine Schülerin eine ihr von mir gestellte Aufgabe behandelt. Wie Sie, verehrter Kollege, wissen, habe ich vor Jahren Herrn Koenigsberger brieflich eine Mitteilung gemacht über die Bedingungen, die eine algebraische Funktion φ (x) erfüllen muß, wenn unter den Integralen

Es sei

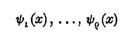
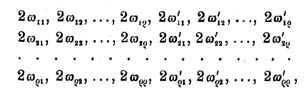
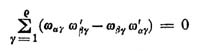
Wenn (ρ > l vorausgesetzt) unter den Integralen   ∫ F (x,φ(x)) dx, es überhaupt eins geben soll, welches in ein elliptisches transformierbar ist, so gibt es auch eins von der Form

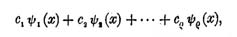
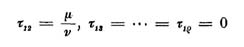
Bildet man mit diesen τ_αβ die Funktion

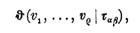
Koenigsberger hat a. a. O. den Fall, wo ρ = 2 und ν = 2 ist, vollständig behandelt. Ich wünschte dasselbe auch für ρ = 3, ν = 2 ausgeführt zu sehen, und meine Schülerin hat diese Arbeit zu meiner vollen Zufriedenheit fertig gebracht. Es gehörte dazu allerdings weniger Erfindungsgabe, aber, wie Sie zugeben werden, eine gründliche Kenntnis der Theorie der Abelschen Funktionen, mit denen sich Frau von Kowalewsky allerdings vollkommen vertraut gemacht hat.

Hiernach, glaube ich, werden Sie sich ein Urteil zu bilden imstande sein, ob Sie das Gesuch meiner Schülerin bei Ihrer Fakultät zu befürworten mit den Anforderungen, welche dieselbe an einen in absentia zu Promovierenden zu stellen pflegt, für vereinbar halten. Ich meinerseits würde kein Bedenken tragen, jede der genannten Arbeiten als Doktordissertation zuzulassen. Da es aber das .erste Mal ist, daß eine Frau auf Grund mathematischer Arbeiten promoviert zu werden wünscht, so hat nicht nur die Fakultät alle Veranlassung, strenge Forderungen zu stellen, sondern es liegt dies auch im Interesse der Aspirantin sowohl als in meinem. Ich bitte daher ausdrücklich, bei der Entscheidung über die Angelegenheit darauf, daß ich beteiligt bin, keinerlei Gewicht zu legen.

Was den Stand der mathematischen Bildung der Frau von Kowalewsky überhaupt angeht, so kann ich versichern, daß ich nur sehr wenige Schüler gehabt habe, die sich, was Auffassungsgabe, Urteil, Eifer und Begeisterung für die Wissenschaft angeht, mit ihr vergleichen ließen.

Jede sonstige Bürgschaft, die etwa inbetreff ihrer verlangt werden möchte, bin ich bereit zu übernehmen. Ausdrücklich hervorheben möchte ich aber, daß sie niemals mit den russischen Studentinnen, die in den letzten Jahren in Zürich und anderswo nicht sehr Erbauliches getrieben haben, in irgend einer Verbindung gestanden hat.

Außer ihr wird sich auch noch eine Chemikerin, Fräulein v. LERMONTOFF, die stets mit ihr zusammen gewesen ist, zur Promotion melden. Dieselbe hat nach HOFMANNS Mitteilung (der ihretwegen an WÖHLER schreiben wird) eine ganz vorzügliche chemische Arbeit geliefert.

Schließlich bitte ich Sie nun, lieber Herr Kollege, mich möglichst bald davon in Kenntnis setzen zu wollen, wann der letzte Termin ist, bis zu welchem die Arbeiten eingeliefert werden müssen, nachdem Sie sich versichert haben, daß dieselben nicht überhaupt zurückgewiesen werden. Sie sind im wesentlichen fertig, bedürfen aber, da die deutsche Sprache der Verfasserin doch sehr große. Schwierigkeiten macht, noch der letzten Feile. Bis zum 15. Juli, glaube ich aber, können sie ablieferbar sein.

Auch den Betrag der Promotionsgebühren wollen Sie mir gefälligst angeben, sowie, was sonst zu tun ist, z. B. ob es zweckmäßig sein würde, wenn ich auch dem Dekan der Fakultät schriebe, dem Sie übrigens auch zu seiner vorläufigen Orientierung dieses mein Schreiben vorlegen können.

Was ich Ihnen sonst noch mitzuteilen hätte, verspare ich mir auf meinen nächsten Brief und schließe diesen über das Maß gewachsenen mit dem aufrichtigen Wunsche, daß Ihnen Göttingen recht bald eine liebe Heimat werde und Ihre Wirksamkeit an einer Universität, mit der sich, was altbegründeten mathematischen Ruhm betrifft, keine andere messen kann, sich zu einer in jeder Beziehung Sie befriedigenden gestalten möge.

Mit freundlichstem Gruß
	der Ihrige
		WEIERSTRASS.

Berlin, 3. Juli 1874.

Was, Sie in Ihrem Schreiben vom 30. mir mitgeteilt haben, hat mich insofern einigermaßen überrascht, als ich erwartet hatte, daß vielleicht das Geschlecht meiner Schülerin, nicht aber der Umstand,, daß sie kein Amt bekleidet, — auf ein solches auch, etwa an einer in Petersburg zu errichtenden Akademie für junge Damen, nicht lossteuert — , ihrer Zulassung zur Promotion in absentia entgegenstehen würde. Ich glaube doch zu wissen, daß noch vor nicht langer Zeit Ausländer in Göttingen in absentia promoviert worden sind, ohne daß sie beamtet gewesen wären; auch hat mir Kollege W. Weber, mit dem ich ausführlich über die Sache sprach, nichts von der fraglichen Bedingung gesagt. Indes ist das eine Frage, über welche der Fakultätsäusschuß ja entscheiden wird.

Einer mündlichen Prüfung in Göttingen sich zu unterziehen würde ich der Frau von Kowalewsky widerraten, nicht etwa weil ich ihr nicht die erforderlichen Kenntnisse zutraue, — sie ist, wie ich wiederhole, im Gegenteil in der Mathematik und auch in verschiedenen Teilen der Physik so gut bewandert wie selten ein Kandidat —, sondern aus einem anderen Grunde. Dieselbe hat bisher ein durchaus zurückgezogenes, ausschließlich ihren Studien gewidmetes Leben geführt. Hier in Berlin hat sie einzig und allein mit mir verkehrt (während ihre mit ihr zusammenwohnende Freundin Fräulein Lermontoff im Hofmannschen Privatlaboratorium gearbeitet hat und so etwas mehr mit Menschen in Berührung gekommen ist). Als eine Folge davon hat sich bei ihr eine Scheu, mit fremden Personen unbefangen zu sprechen, ausgebildet, wozu noch kommt, daß ihr bei ihrer ungewöhnlichen geistigen Beweglichkeit die Gedanken viel rascher zuströmen als sie dieselben in der ihr fremden deutschen Sprache, — in welcher sie sich schriftlich ganz gut auszudrücken versteht —, in Worte zu kleiden imstande ist. Nun brauche ich Ihnen nicht zu sagen, daß ein Kandidat sehr gut vorbereitet sein kann und doch auf manche, Einzelheiten betreffende Frage die Antwort schuldig bleiben muß. Ein junger Mann, der in der Regel schon mehrere Prüfungen bestanden hat, kommt darüber gewöhnlich weg, — obwohl auch Beispiele vom Gegenteil nicht selten sind —, meine Schülerin dagegen würde, wenn der Fall vorkäme, daß sie gleich im Anfang irgend eine Frage nicht beantworten könnte, was doch bei Examinatoren, die den Gang ihrer Studien nicht kennen, leicht möglich wäre, schon durch die ganze ihr ungewohnte Situation aufgeregt, so konsterniert werden, daß der Ausfall der Prüfung schwerlich im Einklang stehen würde mit dem, was sie wirklich weiß. Dieser Gefahr möchte ich sie aber nicht ausgesetzt sehen, zumal da bei ihr keine äußere Nötigung vorliegt, daß sie promoviere. Doch habe ich den dringenden Wunsch, daß ihr dies ermöglicht werde. Der bei einer jungen, in glänzenden Verhältnissen lebenden Dame so ungewöhnliche Entschluß, Mathematik zu studieren — und zwar mit dem vollen Bewußtsein dessen, was dieser Entschluß ihr kosten werde — hat natürlich anfangs bei ihren Angehörigen viel Widerstand gefunden, — ich bemerke bei dieser Gelegenheit, ihr Vater ist der russische Generallieatenant und Gutsbesitzer v. CORVIN-KRUKOWSKY, ihr Urgroßvater mütterlicher Seite war der bekannte Petersburger Astronom und Mathematiker SCHUBERT, ihr Großvater der General und Geodät gleichen Namens (das mathematische Talent ist in der Familie erblich). Es muß ihr daher daran liegen, jetzt, wo sie im Begriff steht, nach einem fünfjährigen Studenten- oder Zigeunerleben, wie sie es selbst nennt, wenn ihr der Mangel des gewohnten häuslichen Komforts doch einmal zu fühlbar wird, in ihr Vaterland und das Familienleben zurückzukehren, nun auch in einer jedermann faßbaren Weise zu dokumentieren, daß es nicht irgend eine Grille, sondern ein wirklicher wissenschaftlicher Drang gewesen ist, von dem getrieben sie unter Verzichtleistung auf alles, was sonst für ein junges weibliches Wesen (sie ist jetzt 23 Jahre alt) Reiz hat, mit einer Energie des Willens, die in einem kaum erklärbaren Gegensatz zu ihrer sonst durchaus weiblichen Natur steht, ihren Entschluß durchgeführt hat. Ich habe geglaubt, Ihnen dies mitteilen zu müssen, obwohl Sie schon durch Freund Koenigsberger manches wissen werden, um hervorzuheben, daß es sich im vorliegenden Falle um eine Persönlichkeit handelt, von der ich überzeugt bin, daß sie eine Zukunft habe und welche promoviert zu haben der Göttinger Universität niemals zur Unehre gereichen würde. Sie wissen von mir, daß ich ein Gegner der Zulassung von Frauen zu den Universitätsstudien (oder vielmehr zum Studieren auf unseren Universitäten) bin, ebenso nicht in dem Rufe stehe, bei Prüfungen den Examinanden es leicht zu machen; Sie können also überzeugt sein, daß es in diesem Falle gewichtige Gründe sein müssen, die mich bestimmen, für die Promotion in absentia einer Frau mich interessieren.

Sollte aber wirklich eine solche nach Ihren Statuten nicht zulässig sein, so würde Frau von Kowalewsky schwerlich bei einer anderen Universität den Versuch wiederholen, — sie hat mir mit Bestimmtheit erklärt, daß sie den Doktortitel sich nur von einer Universität wünsche, welche als eine in rebus mathematicis durchaus kompetente anerkannt sei. Ich würde ihr dann raten, noch eine oder die andere Arbeit, mit deren Plan sie sich herumträgt, zu vollenden, die jetzt fertigen aber in unser Journal aufnehmen; ich glaube, dann nicht lange um eine Universität verlegen sein zu brauchen, die Frau von Kowalewsky honoris causa promovieren würde, eine Auszeichnung, welche die Ihrer Fakultät vorzulegenden Arbeiten, wie ich unter Beziehung auf eine Stelle Ihres Briefes ausdrücklich bemerke, allerdings noch nicht verdienen würden.

Schließlich bemerke ich, daß Frau von Kowalewsky die beiden ersten Arbeiten, die ich Ihnen bezeichnet habe, schon bis zum 15. d. M. würde einsenden können, die dritte einige Tage später.

Sollte die Entscheidung des Fakultätsausschusses günstig lauten, so werden Sie wohl die Güte haben, mir mitzuteilen, in welcher Form die Meldung erfolgen muß.

Mit freundlichstem Gruß
	Ihr ganz ergebener
		WEIERSTRASS

Berlin, 19. Juli 1874.

Sie sehen, wir haben uns ganz nach dem gerichtet, was Sie in Ihren beiden letzten Briefen vorzuschlagen die Güte hatten. Von LOTZE habe ich, ohne mich an ihn gewandt zu haben, ein sehr entgegenkommendes Schreiben erhalten, dessen Inhalt vollkommen mit dem Ihrigen in Einklang steht. Selbstverständlich habe ich ihm sofort geantwortet und für seine Freundlichkeit aufrichtig gedankt.

Ihr letzter Brief hat die Absendung der Abhandlungen insofern einigermaßen verzögert, als es nach demselben geraten schien, gleichzeitig mit der Abhandlung ,,Zur Theorie der partiellen Differentialgleichungen'' die auf die Gestalt der Saturnsringe sich beziehende abgehen zu lassen. Diese ist mit Weglassung der weitläufigen Rechnungen, deren ausführliche Mitteilung für den beabsichtigten Zweck überflüssig und die Beurteilung erschwerend erschien, so gefaßt, daß Weber sehr wohl darüber ein Urteil wird abgeben können, was der Sache nur förderlich sein kann.

Die andere Abhandlung wird wohl zunächst Ihnen vorgelegt werden. Da Sie besser als mancher andere wissen, von welcher Bedeutung schon für die Behandlung der durch eine gewöhnliche Differentialgleichung definierten Funktionen einer Veränderlichen der Satz ist, daß eine der Differentialgleichung formell genügende gewöhnliche Potenzreihe auch stets innerhalb eines gewissen Bezirks konvergiert, so bin ich sicher, daß Sie es als eine anerkennenswerte Leistung betrachten werden, wenn in der in Rede stehenden Abhandlung nunmehr festgestellt worden ist, inwieweit dieser Satz auch für partielle Differentialgleichungen gilt. Ich erlaube mir Sie ganz besonders auf den Umstand aufmerksam zu machen, daß die Gültigkeit dieses Satzes, was mich sehr überrascht hat, von einer bestimmten normalen Form der Differentialgleichung — oder, wenn mehrere Funktionen zu bestimmen sind, des Systems von Differentialgleichungen — abhängt, einer Form, übrigens, die stets durch eine einfache (lineare) Transformation der unabhängigen Veränderlichen erreicht werden kann. Dadurch werden zugleich einige Paradoxa, welche die Theorie der partiellen Differentialgleichungen in Beziehung auf die Zahl der in ihrem allgemeinen Integrale vorkommenden willkürlichen Funktionen darbietet, befriedigend aufgeklärt.

Frau v. Kowalewsky hat mich beauftragt, Ihnen für die Freundlichkeit, mit der Sie sich ihrer Angelegenheit angenommen haben, ihren aufrichtigsten Dank auszusprechen. Noch ein Wort über das curriculum vitae. Frau von Kowalewsky sowohl als Frl. Lermontoff hat Latein gelernt, sodaß die lateinische mathematische Literatur ihr zugänglich ist. Im Schreiben hat sie aber keine Übung und hat sich daher bei Abfassung ihres Elaborates von einem Philologen helfen lassen. Das können Sie nötigenfalls bei Gelegenheit bemerken. Ich bin unschuldig daran.

Freundlichst grüßend
	WEIERSTRASS.

Berlin, 21. Juli 1874.

Da ich Sie nun doch noch einmal mit einem Briefe behelligen muß, so erlaube ich mir noch zwei Punkte zu berühren. Sollte die Promotionskommission dem Gesuche der Frau von Kowalewsky, so, wie es gestellt ist, nicht willfahren zu können glauben, so würde es ihr lieb sein, wenn sie nicht etwa ihres Geschlechtes wegen einfach abgewiesen, sondern ihr das Bestehen einer mündlichen Prüfung zur Bedingung gemacht würde. Vielleicht überwände sie doch noch — namentlich, nachdem die Arbeiten angenommen wären — ihre Scheu und würde zu Anfang des nächsten Semesters sich zur Prüfung stellen. Ich habe an Lotze dasselbe schon früher geschrieben, möchte aber allerdings dringend wünschen, daß die Sache sich in der beantragten Weise abmachen ließe. Ich fürchte nämlich auch, daß die junge, sehr zart gebaute Frau, die begreiflicherweise durch ein Examen weit mehr aufgeregt wird wie ein schon durch verschiedene Prüfungen abgehärteter Student und der man jetzt schon die Anstrengung der letzten Monate ansieht, zu sehr würde angegriffen werden, wenn sie noch mehrere Monate in beständiger Spannung leben müßte. Wird das examen rigorosum erlassen, so haben Sie wohl die Güte, sich bei dem Dekan nach dem Betrag der Gebühren und dem Einsendungstermin zu erkundigen.

Die Arbeit ,,Zur Theorie der partiellen Differentialgleichungen'' betreffend möchte ich noch bemerken, daß ursprünglich die Absicht war, noch eine Beilage ,,Anwendungen und Folgerungen'' hinzuzufügen. Aber die Ausarbeitung macht große Mühe, und so ist dieser Abschnitt vorläufig zurückgestellt. Er enthält aber manches Interessante. Z.B.: Wenn ein homogener Körper von einer regulären (analytischen) Fläche S begrenzt ist und man konstruiert zwei Parallelflächen S₁, S₂ derselben, die erstere innerhalb, die andere außerhalb des Körpers, doch so, daß in dem Raum zwischen S₁ und S₂ kein Krümmungsmittelpunkt von S liegt, so läßt sich das äußere Potential des Körpers stets bis zur Fläche S₁ das innere bis zur Fläche S₂ fortsetzen (als eindeutige analytische Funktion der Koordinaten). Daraus folgt u. a.: Wenn die Fläche S von einer Kugelfläche wenig abweicht — in einem noch genauer zu bestimmenden Sinne —, so gilt die Reihe, in welche sich das innere Potential unter der Voraussetzung, daß der angezogene Punkt nahe beim Schwerpunkt des Körpers liegt, entwickeln läßt, auch noch über S hinaus, ebenso die Entwicklung des äußeren Potentials, die unter der Voraussetzung erhalten wird, daß der angezogene Punkt vom Schwerpunkt weit entfernt liegt, auch noch für Punkte auf der Innenseite von S. Damit läßt sich dann der berühmte Legendresche Satz über die Gestalt einer rotierenden homogenen Flüssigkeit, wenn dieselbe von der Kugelgestalt wenig abweicht — nämlich daß die Oberfläche dann notwendig ein Rotationsellipsoid sei — strenge beweisen, was von Legendre keineswegs geschehen ist, wenigstens nicht unseren heutigen Anforderungen entsprechend. — Sie werden zugeben, daß ein Student, der sich mit derartigen Untersuchungen ganz selbständig beschäftigt, nicht eine gewöhnliche Erscheinung ist.

WEIERSTRASS.     

Letzte Änderung: Mai 2014     Gabriele Dörflinger   Kontakt

Zur Inhaltsübersicht     Historia Mathematica     Homo Heidelbergensis