Brief von Carl Weierstraß an Lazarus Fuchs
bezgl. der Dissertation S. Kowalewskajas

Berlin, 27. Juni 1874.

Verehrter Freund und Kollege!

Zunächst habe ich Ihnen meinen verbindlichsten Dank für die Bereitwilligkeit auszusprechen, mit der Sie sich sofort nach Ihrer Ankunft in Göttingen der Mühe unterzogen haben, mir inbetreff der Promotionsangelegenheit meiner Schülerin, der Frau VON KOWALEWSKY, die gewünschte Auskunft zu verschaffen. Was Sie in Ihrem Briefe vom 18. April d. J. mir mitteilen, ist mir unmittelbar darauf von Herrn Prof. Weber, den hier in Berlin einmal wieder sprechen zu können mir eine große Freude gewesen ist, vollständig bestätigt worden, wobei ich von demselben noch die interessante Notiz erhielt, daß Gauß, als es sich bei Gelegenheit der letzten Jubelfeier der Göttinger Universität um die zu vollziehenden Ehrenpromotionen handelte, nichts mehr bedauert habe, als daß Sophie Germain nicht mehr am Leben sei, welche der Welt bewiesen habe, daß auch eine Frau in der strengsten und abstraktesten der Wissenschaften etwas Tüchtiges zu leisten imstande sei und darum ein Ehrendiplom wohl verdient haben würde.

Hiernach habe ich kein Bedenken getragen, Frau von Kowalewsky zu ermutigen, sich bei Ihrer Fakultät um die Promotion in absentia zu bewerben und zu dem Zweck einige Arbeiten, mit denen sie sich im letzten Jahre teils aus eigenem Antrieb, teils auf meine Veranlassung beschäftigt hat, fertig zu machen. Auf meinen Rat wird sie der Fakultät drei Abhandlungen vorlegen, um den Beweis zu liefern, daß sie auf verschiedenen Gebieten der Mathematik heimisch genug geworden ist, um im Anschluß an Vorhandenes selbständige und für die Wissenschaft ersprießliche Untersuchungen anzustellen. Eine dieser Abhandlungen beschäftigt sich mit der Frage, ob und wie weit sich die Sätze über die Integration eines Systems gewöhnlicher Differentialgleichungen durch Potenzreihen, welche ich zuerst in meiner Abhandlung über die analytischen Fakultäten (Crelles Journal 51, S, 43,44) aufgestellt habe und die bald darauf von den Herren Briot und Bouquet bewiesen worden sind, auf den Fall ausdehnen lassen, wo zur Bestimmung von Funktionen mehrerer Veränderlichen die erforderliche Anzahl von partiellen Differentialgleichungen gegeben ist. Die Frage mußte unbedingt einmal gründlich erörtert werden; ich selbst habe, offen gestanden, Scheu gehabt, mich darauf einzulassen, und es freut mich umso mehr, daß sie in der in Rede stehenden Arbeit, die in ihrer letzten Redaktion nur von mäßigem Umfange ist, auf die gründlichste Weise erledigt worden ist. Schwierigkeiten, die sich zunächst darboten, z. B. die unerwartete und Bedenken erregende Bemerkung, daß schon eine so einfache Differentialgleichung, wie die so oft behandelte

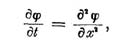
wenn man festsetzt, daß φ (x, t) für t = 0 in eine gegebene, durch eine konvergierende Potenzreihe von x darstellbare Funktion φ0 (x) übergehen soll, im allgemeinen, d. h. wenn φ0(x) nicht ganz besondere Bedingungen erfüllt, zu einer stets divergierenden Entwickelung von φ0(x,t) nach Potenzen von t führt, sind durch den Scharfsinn der Verfasserin auf die einfachste und befriedigendste Weise beseitigt worden. Ich bin überzeugt, diese Arbeit wird auch Ihr Interesse erregen.

In der zweiten Abhandlung sind die LAPLACEschen Untersuchungen über die Gestalt der Saturnsringe wieder aufgenommen und weitergeführt worden. Die Resultate von Laplace sind nur als erste Annäherung betrachtet gültig; ein Ring, der den Bedingungen des Problems, wie es von Laplace gestellt ist, genügen soll, kann nicht durch Umdrehung einer Ellipse um eine ihrer kleinen Axe parallele Gerade entstanden sein; an die Stelle der Ellipse muß vielmehr eine Figur treten, welche an ihren beiden Scheiteln verschieden gekrümmt ist und sich auch unter der von Laplace gemachten Annahme, wenn man von der Komplikation der Rechnung absieht, bis zu jedem Grade der Annäherung bestimmen läßt. Für die zweite Annäherung ist die Rechnung vollständig ausgeführt.

In einer dritten Abhandlung hat meine Schülerin eine ihr von mir gestellte Aufgabe behandelt. Wie Sie, verehrter Kollege, wissen, habe ich vor Jahren Herrn Koenigsberger brieflich eine Mitteilung gemacht über die Bedingungen, die eine algebraische Funktion φ (x) erfüllen muß, wenn unter den Integralen

∫ F (x,φ(x)) dx,
wo F eine rationale Funktion von x und φ (x) bedeutet, solche sich finden sollen, die sich in elliptische Integrale transformieren lassen. (Koenigsberger erwähnt diese Mitteilung in einer seiner Arbeiten über die Transformation der Abelschen Funktionen). Vollständiger ausgesprochen lautet der betreffende Satz folgendermaßen.

Es sei

ein vollständiges System von Abelschen Integralen erster Gattung, deren Ableitungen sich rational durch x und φ (x) ausdrücken lassen. Dann gibt es bekanntlich unendlich viele primitive Perioden-Systeme dieser Integrale
für welche die Gleichungen
bestehen.

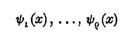
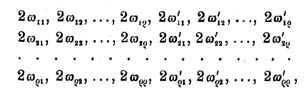
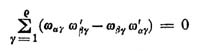
Wenn (ρ > l vorausgesetzt) unter den Integralen   ∫ F (x,φ(x)) dx, es überhaupt eins geben soll, welches in ein elliptisches transformierbar ist, so gibt es auch eins von der Form

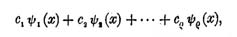
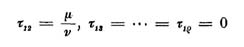
und damit dieses existiere, ist notwendig und hinreichend, daß unter jenen Periodensystemen sich eines finde, für welches von den daraus abgeleiteten, von mir mit ταβ bezeichneten Größen
sind, wo μ,ν ganze positive Zahlen (ohne gemeinsamen Teiler) bedeuten.

Bildet man mit diesen ταβ die Funktion

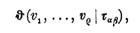
so sieht man sofort, daß unter den daraus durch eine Transformation ν ten Grades sich ergebenden ϑ-Funktionen eine die Eigenschaft hat, in ein Produkt einer ϑ- Funktion von (ρ - 1) Argumenten und einer elliptischen zu zerfallen. Dadurch wird man in den Stand gesetzt, die algebraischen Relationen, die unter den Konstanten der Funktion von φ(x) stattfinden, zu ermitteln.

Koenigsberger hat a. a. O. den Fall, wo ρ = 2 und ν = 2 ist, vollständig behandelt. Ich wünschte dasselbe auch für ρ = 3, ν = 2 ausgeführt zu sehen, und meine Schülerin hat diese Arbeit zu meiner vollen Zufriedenheit fertig gebracht. Es gehörte dazu allerdings weniger Erfindungsgabe, aber, wie Sie zugeben werden, eine gründliche Kenntnis der Theorie der Abelschen Funktionen, mit denen sich Frau von Kowalewsky allerdings vollkommen vertraut gemacht hat.

Hiernach, glaube ich, werden Sie sich ein Urteil zu bilden imstande sein, ob Sie das Gesuch meiner Schülerin bei Ihrer Fakultät zu befürworten mit den Anforderungen, welche dieselbe an einen in absentia zu Promovierenden zu stellen pflegt, für vereinbar halten. Ich meinerseits würde kein Bedenken tragen, jede der genannten Arbeiten als Doktordissertation zuzulassen. Da es aber das .erste Mal ist, daß eine Frau auf Grund mathematischer Arbeiten promoviert zu werden wünscht, so hat nicht nur die Fakultät alle Veranlassung, strenge Forderungen zu stellen, sondern es liegt dies auch im Interesse der Aspirantin sowohl als in meinem. Ich bitte daher ausdrücklich, bei der Entscheidung über die Angelegenheit darauf, daß ich beteiligt bin, keinerlei Gewicht zu legen.

Was den Stand der mathematischen Bildung der Frau von Kowalewsky überhaupt angeht, so kann ich versichern, daß ich nur sehr wenige Schüler gehabt habe, die sich, was Auffassungsgabe, Urteil, Eifer und Begeisterung für die Wissenschaft angeht, mit ihr vergleichen ließen.

Jede sonstige Bürgschaft, die etwa inbetreff ihrer verlangt werden möchte, bin ich bereit zu übernehmen. Ausdrücklich hervorheben möchte ich aber, daß sie niemals mit den russischen Studentinnen, die in den letzten Jahren in Zürich und anderswo nicht sehr Erbauliches getrieben haben, in irgend einer Verbindung gestanden hat.

Außer ihr wird sich auch noch eine Chemikerin, Fräulein v. LERMONTOFF, die stets mit ihr zusammen gewesen ist, zur Promotion melden. Dieselbe hat nach HOFMANNS Mitteilung (der ihretwegen an WÖHLER schreiben wird) eine ganz vorzügliche chemische Arbeit geliefert.

Schließlich bitte ich Sie nun, lieber Herr Kollege, mich möglichst bald davon in Kenntnis setzen zu wollen, wann der letzte Termin ist, bis zu welchem die Arbeiten eingeliefert werden müssen, nachdem Sie sich versichert haben, daß dieselben nicht überhaupt zurückgewiesen werden. Sie sind im wesentlichen fertig, bedürfen aber, da die deutsche Sprache der Verfasserin doch sehr große. Schwierigkeiten macht, noch der letzten Feile. Bis zum 15. Juli, glaube ich aber, können sie ablieferbar sein.

Auch den Betrag der Promotionsgebühren wollen Sie mir gefälligst angeben, sowie, was sonst zu tun ist, z. B. ob es zweckmäßig sein würde, wenn ich auch dem Dekan der Fakultät schriebe, dem Sie übrigens auch zu seiner vorläufigen Orientierung dieses mein Schreiben vorlegen können.

Was ich Ihnen sonst noch mitzuteilen hätte, verspare ich mir auf meinen nächsten Brief und schließe diesen über das Maß gewachsenen mit dem aufrichtigen Wunsche, daß Ihnen Göttingen recht bald eine liebe Heimat werde und Ihre Wirksamkeit an einer Universität, mit der sich, was altbegründeten mathematischen Ruhm betrifft, keine andere messen kann, sich zu einer in jeder Beziehung Sie befriedigenden gestalten möge.

Mit freundlichstem Gruß
 der Ihrige
  WEIERSTRASS.

Weierstraß, Carl:
Briefe von K. Weierstrass an L. Fuchs
In: Acta mathematica. - 39 (1923), S. 246-250
Signatur UB Heidelberg: L 15-6::39.1923

Letzte Änderung: Mai 2014     Gabriele Dörflinger   Kontakt

Zur Inhaltsübersicht     Historia Mathematica     Homo Heidelbergensis