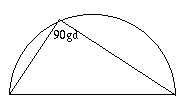
Historia Mathematica Heidelbergensis 

Ein paar Klassiker

Sie finden auf dieser Seite Informationen zu folgenden mathematischen Problemen

Der Satz des Thales

Der Peripheriewinkel des Halbkreisbogens beträgt 90 Grad.

Alter Beweis:
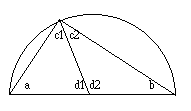
Zeichnet man die Verbindung vom Mittelpunkt der Hypothenuse auf die Spitze des Dreiecks, so sind die beiden entstehenden Dreiecke gleichschenklig. Deshalb sind auch die Winkel a und c1, sowie b und c2 gleich. Da die Summe der Winkel im Dreieck 180° beträgt, haben wir a + b + (c1 + c2) = 180° und wegen a = c1 und b = c2 ergibt sich c = c1 + c2 = 90°.

Es wird im allgemeinen angenommen, dass die Beweise im 6. Jahrhundert vor Christus eher ein Zeigen, denn ein strenges logisches Schließen waren. Immerhin war Thales nach der Überlieferung bekannt, dass die Basiswinkel im gleichschenkligen Dreieck gleich sind.

Thales von Milet 625 v. Chr. - 547 v.Chr.

Der Satz des Pythagoras

Im rechtwinkligen Dreieck ist die Summe der Quadrate über die Katheten gleich dem Quadrat über die Hypothenuse.
a2 + b2 = c2

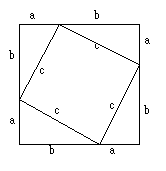
Antiker Beweis: Man betrachte das Quadrat (a + b)2
Es hat einerseits den Inhalt a2 + b2 + 2ab. Andererseits besteht es aus dem kleinen Quadrat mit der Seitenlänge c und vier mal dem rechtwinkligen Dreieck in den Ecken des grossen Quadrats.
Dies ergibt den Flächeninhalt c2 + 4 * (ab/2) = c2 + 2ab.

Euklid verwendete in seinen Elementen einen anderen Beweis.

Mario Gerwig publizierte 1921 bei Springer Spektrum eine Beweissammlung mit 365 Beweisen (Der Satz des Pythagoras in 365 Beweisen. ISBN 978-3-662-62885-0)
Im Internet werden von Interactive Mathematics Miscellany and Puzzles 122 Beweise angeboten.

Pythagoras ca. 580 - 500 v. Chr.

Achill und die Schildkröte / Zenon von Elea

Das langsamste, die Schildkröte, könnte von dem schnellsten, von Achill, nicht eingeholt werden, wenn sie irgend einen Vorsprung vor ihm hat. Denn um sie einzuholen, müsste Achill erst an den Punkt kommen, wo sie sich befand, als er anfing zu laufen, dann an den, bis wohin sie in der Zwischenzeit fortgerückt ist, dann dahin, wohin sie gelangte, während er diesen zweiten Vorsprung einbrachte, und so fort in's unendliche.
(Zeller, Eduard: Die Philosophie der Griechen in ihrer geschichtlichen Entwicklung, Bd. 1,1 1892, S. 596)

Bereits Aristoteles bemerkte, dass die Zeit in gleicher Weise wie der Raum geteilt wird. Somit stehen für die unendlich vielen Wegintervalle auch unendlich viele Zeitintervalle zur Verfügung.

Zenon von Elea ca. 490 v. Chr. - 430 v. Chr.

Euklid: Es gibt unendlich viele Primzahlen

Nehmen wir an, es gibt nur n Primzahlen. Dann bilden wir das Produkt aller Primzahlen und addieren 1.
p1*p2*···*pn + 1 = a
Da a nach Voraussetzung mindestens einen Primzahlteiler hat und das Produkt ebenso diesen Teiler hat, muss auch 1 diesen Teiler haben. Damit sind wir zum Widerspruch gelangt.

Euklid ca. 325 v. Chr. - 265 v. Chr.

Der grosse Satz von Fermat

Die Gleichung
an + bn = cn
für natürliche Zahlen a, b, c, und n ist für n > 2 nicht lösbar.

Fermat schrieb an den Rand von Diophants Arithmetica.

Es ist unmöglich, einen Kubus in zwei Kuben zu teilen, eine vierte Potenz in zwei vierte Potenzen, oder allgemeiner gesagt, irgendeine Potenz über der zweiten in zwei Potenzen des gleichen Grades: Ich habe eine wahrhaft wunderbare Beweisführung (dieses allgemeinen Satzes) entdeckt, der auf diesen Rand nicht Platz findet.
(Meschkowski, Herbert: Mathematiker-Lexikon, 1964, S. 86)

Dieser Satz konnte in der Vergangenheit zwar für viele n, aber nicht allgemein bewiesen werden.

1910 setzte die Wolfskehl-Stiftung einen Preis aus.

Preis der Wolfskehl-Stiftung. Die Königliche Gesellschaft der Wissenschaften in Göttingen hat auf Grund des von dem verstorbenen Herrn Dr. Paul Wolfskehl in Darmstadt ihr zugewendeten Vermächtnisses einen Preis von 100000 M. für denjenigen ausgesetzt, dem es zuerst gelingt, den Beweis des großen Fermatschen Satzes zu führen. Die bezügliche Bekanntmachung ist in den geschäftlichen Mitteilungen veröffentlicht worden.
(Aus dem Jahresbericht der Deutschen Mathematiker-Vereinigung, 1911)

1995 gelang Andrew Wiles mit Richard Taylor der Beweis. (veröffentlicht in Annals of Mathematics 141 (1995) 443-551 und 553-572)

Berichte dazu:
Bild der Wissenschaft, 1997/10
Spektrum der Wissenschaft, 1998/1
Kramer, Jürg: Der große Satz von Fermat
In: Alles Mathematik / M. Aigner und E. Behrends (Hrsg.) - 2000, S. 169-179
    Signatur UB Heidelberg: 2000 H 518
Singh, Simon: Fermats letzter Satz. - München, 1998
    Signatur UB Heidelberg: 98 H 409
Koch, Helmut: Geschichte und Beweis der Fermatschen Vermutung
In: Jahrbuch der Heidelberger Akademie der Wissenschaften. - 1998, S. 135-140
    Signatur UB Heidelberg: ZSA 889 B::1998
  Roquette, Peter: Zum Fermat-Problem, 1998

Pierre Fermat 1601 - 1665

Die Goldbachsche Vermutung

Jede gerade Zahl ist als Summe zweier Primzahlen darstellbar
(immer noch nicht bewiesen)

Christian Goldbach 18.3.1690 - 12.1.1764

Das Königsberger Brückenproblem / Leonhard Euler

Königsberg liegt auf zwei Inseln und den beiden Ufern des Pregels. Es ist nicht möglich, bei einem Spaziergang über alle Brücken einmal und nur einmal zu gehen.

Beweis:
Der Weg lässt sich als Graph mit Knoten auf den beiden Inseln und Ufern darstellen. Da ich jeden Knoten, den ich betrete, auch wieder verlassen muss, muss eine gerade Anzahl von Kanten (= Brücken) auf den Knoten führen. Dies ist nicht der Fall.

Euler kam aus Basel und arbeitete in Berlin und Petersburg. Er war nie in Königsberg tätig. Er stand aber in Kontakt mit Christian Goldbach, der aus Königsberg gebürtig war. Vielleicht kam daher seine Kenntnis der Königsberger Brücken.

Eine schönere Darstellung der Königsberger Brücken als obige Zeichnung, nämlich eine Bearbeitung der Radierung von Matthäus Merian, und eine vertiefte Darstellung des Problems ist im Netz der Universität Wuppertal erhältlich.

Leonhard Euler 4.4.1707 - 18.9.1783

Letzte Änderung: 22.11.2023     Gabriele Dörflinger

  Startseite       Kontakt